Difference between revisions of "Store:46laterotrusivo"
| Line 55: | Line 55: | ||
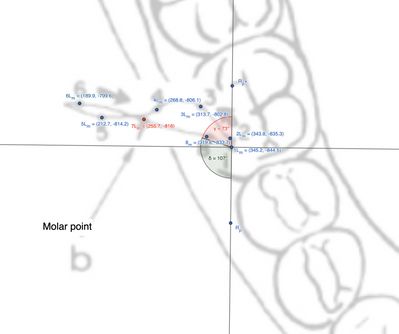
Osservando la figura e la tabella, possiamo estrapolare le distanze e le direzioni dei punti marcati. Nello specifico, la distanza del punto <math>7L_m</math> rispetto al punto iniziale <math>1L_m</math> è stata calcolata come circa <math> | Osservando la figura e la tabella, possiamo estrapolare le distanze e le direzioni dei punti marcati. Nello specifico, la distanza del punto <math>7L_m</math> rispetto al punto iniziale <math>1L_m</math> è stata calcolata come circa <math>3.93 \,_ \text{mm}</math>, con un angolo formato tra i vettori pari a <math>\cong 73 ^\circ</math>. | ||
{{Tooltip|Definizione dei vettori: <math>\vec{AB} = 7L_m - 1L_m = (255.7, -816.0) - (345.2, -844.5) = (-89.5, 28.5)</math>, <math>\vec{AC} = R_p - 1L_m = (346.6, -727.1) - (345.2, -844.5) = (1.4, 117.4)</math>. Magnitudine di <math>\vec{AB}</math>: <math>|\vec{AB}| = \sqrt{(-89.5)^2+(28.5)^2}\approx 93.93</math>, magnitudine di <math>\vec{AC}</math>: <math>|\vec{AC}| = \sqrt{(1.4)^2 + (117.4)^2} \approx 117.41</math>. Prodotto scalare: <math>\vec{AB}\cdot \vec{AC} = (-89.5)(1.4) + (28.5)(117.4) = 2928.4</math>, <math>\cos(\theta) = \frac{\vec{AB} \cdot \vec{AC}}{|\vec{AB}| \cdot |\vec{AC}|} = \frac{2928.4}{93.93 \cdot 117.41} \approx 0.292</math>, angolo: <math>\theta = \arccos(0.292) \approx 73.02^\circ</math>.}} | |||
Revision as of 02:14, 26 December 2024
Molare Laterotrusivo
Il testo descrive un'analisi dettagliata dei movimenti articolari del molare ipsilaterale al condilo laterotrusivo (Figura 6 e Tabella 2). L'analisi si basa sul calcolo delle distanze tra punti e degli angoli formati tra i vettori utilizzando la trigonometria vettoriale.
| Tabella 2 | ||||
|---|---|---|---|---|
| Tracciato masticatorio | Markers | Distanza (mm) | Direzione
(antero-posteriore) |
Direzione dinamica
(latero-mediale) |
| 2 | 0.39 | Indietro | Lateralizzazione | |
| 3 | 2.18 | Indietro | Lateralizzazione | |
| 4 | 3.57 | Indietro | Lateralizzazione | |
| 5 | 5.68 | Indietro | Lateralizzazione | |
| 6 | 6.76 | Indietro | Inversione | |
| 7* | 3.93 | Indietro | Medializzazione | |
| 8 | 1.15 | Indietro | Medializzazione | |
Osservando la figura e la tabella, possiamo estrapolare le distanze e le direzioni dei punti marcati. Nello specifico, la distanza del punto rispetto al punto iniziale è stata calcolata come circa , con un angolo formato tra i vettori pari a .
Definizione dei vettori: , . Magnitudine di : , magnitudine di : . Prodotto scalare: , , angolo: .