Difference between revisions of "Asse Cerniera Verticale"
| Line 58: | Line 58: | ||
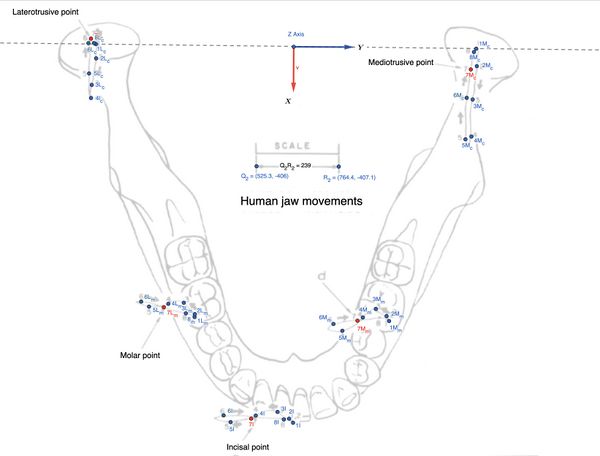
L’analisi dei movimenti condilari richiede misurazioni precise, ottenute tramite **calibrazione dell’immagine**.{{Tooltip|2={{Tooltip|Calcolo della distanza|'''Calcolo della Distanza tra i Punti''' Le coordinate dei punti sono: <math>Q_2(525.3, -406)</math> e <math>R_2(764.4, -407.1)</math>. La formula per la distanza euclidea è: <math>d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}</math>. Sostituendo i valori: <math>d = \sqrt{(764.4 - 525.3)^2 + (-407.1 - (-406))^2}</math>, <math>d = \sqrt{(239.1)^2 + (-1.1)^2}</math>, <math>d = \sqrt{57121.81 + 1.21} = \sqrt{57123.02} \approx 239.02 \, \text{pixel}</math>. '''Conversione della Scala in mm''': Dato che <math>239.02 \, \text{pixel}</math> equivale a <math>1 \, \text{cm} = 10 \, \text{mm}</math>, calcoliamo la conversione in mm/pixel: <math>\text{Scala in mm/pixel} = \frac{\text{Lunghezza reale (in mm)}}{\text{Distanza in pixel}} = \frac{10}{239.02} \approx 0.04184 \, \text{mm/pixel}</math>. Quindi, ogni pixel nella figura corrisponde a circa <math>0.04184 \, \text{mm/pixel}</math>. '''Esempio di Applicazione: Conversione Distanza in mm''' Se <math>d = 100 \, \text{pixel}</math>, allora: <math>d_\text{mm} = 100 \cdot 0.04184 \approx 4.184 \, \text{mm}</math>.}}}} | L’analisi dei movimenti condilari richiede misurazioni precise, ottenute tramite **calibrazione dell’immagine**.{{Tooltip|2={{Tooltip|Calcolo della distanza|'''Calcolo della Distanza tra i Punti''' Le coordinate dei punti sono: <math>Q_2(525.3, -406)</math> e <math>R_2(764.4, -407.1)</math>. La formula per la distanza euclidea è: <math>d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}</math>. Sostituendo i valori: <math>d = \sqrt{(764.4 - 525.3)^2 + (-407.1 - (-406))^2}</math>, <math>d = \sqrt{(239.1)^2 + (-1.1)^2}</math>, <math>d = \sqrt{57121.81 + 1.21} = \sqrt{57123.02} \approx 239.02 \, \text{pixel}</math>. '''Conversione della Scala in mm''': Dato che <math>239.02 \, \text{pixel}</math> equivale a <math>1 \, \text{cm} = 10 \, \text{mm}</math>, calcoliamo la conversione in mm/pixel: <math>\text{Scala in mm/pixel} = \frac{\text{Lunghezza reale (in mm)}}{\text{Distanza in pixel}} = \frac{10}{239.02} \approx 0.04184 \, \text{mm/pixel}</math>. Quindi, ogni pixel nella figura corrisponde a circa <math>0.04184 \, \text{mm/pixel}</math>. '''Esempio di Applicazione: Conversione Distanza in mm''' Se <math>d = 100 \, \text{pixel}</math>, allora: <math>d_\text{mm} = 100 \cdot 0.04184 \approx 4.184 \, \text{mm}</math>.}}}} | ||
'''Fattore di scala utilizzato:'''{{Tooltip|2={{Tooltip|Distanze condilari|'''Calcolo delle distanze tra i punti''' Le coordinate dei punti estrapolate da Geogebra dopo calibrazione, per il condilo laterotrusivo, sono: 1L: <math>(58.3, -50.9)</math>, 2L: <math>(59, -92.3)</math>, 3L: <math>(46.3, -169.5)</math>, 4L: <math>(44.1, -207.7)</math>, 5L: <math>(38.4, -136.2)</math>, 6L: <math>(36.4, -48.2)</math>, 7L: <math>(44, -34.9)</math>, 8L: <math>(52.9, -48)</math>. '''Fattore di scala:''' <math>0.04184 \, \text{mm/pixel}</math>. Distanze rispetto a <math>1L_c | '''Fattore di scala utilizzato:'''{{Tooltip|2={{Tooltip|Distanze condilari|'''Calcolo delle distanze tra i punti''' Le coordinate dei punti estrapolate da Geogebra dopo calibrazione, per il condilo laterotrusivo, sono: 1L: <math>(58.3, -50.9)</math>, 2L: <math>(59, -92.3)</math>, 3L: <math>(46.3, -169.5)</math>, 4L: <math>(44.1, -207.7)</math>, 5L: <math>(38.4, -136.2)</math>, 6L: <math>(36.4, -48.2)</math>, 7L: <math>(44, -34.9)</math>, 8L: <math>(52.9, -48)</math>. '''Fattore di scala:''' <math>0.04184 \, \text{mm/pixel}</math>. Distanze rispetto a <math>1L_c</math>: ''' <math>d = \sqrt{(59 - 58.3)^2 + (-92.3 - (-50.9))^2} \approx 41.41 \, \text{pixel}</math>, <math>d = 41.41 \cdot 0.04184 \approx 1.734 \, \text{mm}</math>. '''<math>2L_c</math>:''' <math>d = \sqrt{(46.3 - 58.3)^2 + (-169.5 - (-50.9))^2} \approx 119.17 \, \text{pixel}</math>, <math>d = 119.17 \cdot 0.04184 \approx 4.99 \, \text{mm}</math>. '''<math>3L_c</math>:''' <math>d = \sqrt{(44.1 - 58.3)^2 + (-207.7 - (-50.9))^2} \approx 157.43 \, \text{pixel}</math>, <math>d = 157.43 \cdot 0.04184 \approx 6.59 \, \text{mm}</math>. '''<math>4L_c</math>:''' <math>d = \sqrt{(38.4 - 58.3)^2 + (-136.2 - (-50.9))^2} \approx 87.6 \, \text{pixel}</math>, <math>d = 87.6 \cdot 0.04184 \approx 3.66 \, \text{mm}</math>. '''<math>5L_c</math>:''' <math>d = \sqrt{(36.4 - 58.3)^2 + (-48.2 - (-50.9))^2} \approx 22.06 \, \text{pixel}</math>, <math>d = 22.06 \cdot 0.04184 \approx 0.923 \, \text{mm}</math>. '''<math>6L_c</math>:''' <math>d = \sqrt{(44 - 58.3)^2 + (-34.9 - (-50.9))^2} \approx 21.47 \, \text{pixel}</math>, <math>d = 21.47 \cdot 0.04184 \approx 0.898 \, \text{mm}</math>. '''<math>7L_c</math>:''' <math>d = \sqrt{(52.9 - 58.3)^2 + (-48 - (-50.9))^2} \approx 6.13 \, \text{pixel}</math>, <math>d = 6.13 \cdot 0.04184 \approx 0.257 \, \text{mm}</math>.<math>8L_c</math>}}}} | ||
***1 cm = 10 mm = 239.02 pixel** | ***1 cm = 10 mm = 239.02 pixel** | ||
***Scala in mm/pixel:** <math>0.04184 \, \text{mm/pixel}</math> | ***Scala in mm/pixel:** <math>0.04184 \, \text{mm/pixel}</math> | ||
Revision as of 11:49, 2 February 2025
Cinematica Mandibolare: Rotazioni e Traslazioni Condilari
Introduzione
Nel capitolo precedente, Transverse Hinge Axis, abbiamo introdotto la cinematica mandibolare analizzandone i movimenti sul piano sagittale. Durante i movimenti di **protrusione** e **retrusione**, la mandibola non si muove esclusivamente lungo l'asse , ma ruota anche attorno all'asse . Questo genera una traiettoria curvilinea dell’incisivo mandibolare, risultato di un complesso moto spaziale che combina **rotazione e traslazione condilare**.
Uno degli aspetti chiave di questa dinamica è lo **spazio libero interincisivo**, una regione angolare che permette movimenti masticatori fluidi e senza interferenze. Tuttavia, gli strumenti di analisi come il **Sirognatograph** e i sistemi elettromagnetici convenzionali ad effetto Hall tendono a focalizzarsi sulle traslazioni condilari, trascurando la componente rotazionale. Sebbene ciò possa essere sufficiente in alcuni contesti, non è adeguato a rappresentare fedelmente i movimenti mandibolari a sei gradi di libertà.
Cinematica Mandibolare a Sei Gradi di Libertà
Il movimento mandibolare si sviluppa in uno **spazio tridimensionale** e può essere descritto attraverso **sei gradi di libertà**, suddivisi in **tre traslazioni** e **tre rotazioni**.
Ogni condilo si muove rispetto ai seguenti **assi principali**:
- Asse (latero-mediale):** definisce la rotazione attorno all’asse cerniera trasversale (, transverse Hinge Axis).
- Asse (verticale):** definisce la rotazione attorno all’asse cerniera verticale ().
- Asse (antero-posteriore):** definisce la rotazione attorno all’asse cerniera orizzontale ().
A ciascun asse corrisponde un **piano di riferimento anatomico**:
- Piano sagittale: mostra il tracciato condilare prodotto dalla **rototraslazione** sull’asse trasversale ().
- Piano coronale: associato all’asse orizzontale ().
- Piano assiale: legato alla rotazione sull’asse verticale ().
Nota: un piano non è generato direttamente da un asse, bensì un asse può essere contenuto in un piano o definirne una direzione. Più precisamente, il movimento di un asse genera una superficie rigata, che rappresenta l’insieme delle traiettorie spaziali risultanti.
Asse Cerniera Verticale e Strumenti di Registrazione
L’**asse cerniera verticale** () è particolarmente rilevante per i sistemi di registrazione cinematici, come:
- Pantografi** (analogici ed elettronici)
- Elettrongnatografi**
- Assiografi**
Strumenti di Registrazione e Precisione
- Il pantografo analogico è stato a lungo considerato un dispositivo preciso per la riproduzione dei tracciati condilari e il loro trasferimento su un articolatore regolabile.[1][2][3]
- Il pantografo elettronico, introdotto successivamente, ha dimostrato una precisione comparabile nella registrazione dei determinanti condilari.[4]
- Un parametro controverso nel movimento condilare è la **traslazione laterale immediata mandibolare** (Movimento di Bennett), il cui significato clinico è stato oggetto di dibattito.[5] Studi recenti indicano che non esistono prove sufficienti a confermare la sua rilevanza clinica.[6]
Nota sulla Precisione e Sugli Obiettivi dello Studio
Questo studio mira a fornire una comprensione concettuale dei principi cinematici coinvolti nella dinamica masticatoria, con un focus sulla biomeccanica mandibolare. Sebbene i calcoli siano stati eseguiti con rigore, potrebbero verificarsi discrepanze dovute a:
- Approssimazioni nei dati numerici: Differenze nei valori cartesiani legate a variabili operative.
- Limiti di rappresentazione: Uso di numeri approssimati per motivi pratici.
- Finalità cliniche: Lo scopo è descrivere concetti piuttosto che ottenere precisione assoluta.
Passi Successivi
In questo capitolo, analizzeremo la cinematica dell'asse verticale () e il fenomeno masticatorio, rappresentandolo con tracciati estratti da lavori di riferimento come quello di Lund e Gibbs.[7](Figura 1)
Misurazioni e Conversione da Pixel a Millimetri
L’analisi dei movimenti condilari richiede misurazioni precise, ottenute tramite **calibrazione dell’immagine**. ![]() Calcolo della distanzaCalcolo della Distanza tra i Punti Le coordinate dei punti sono: e . La formula per la distanza euclidea è: . Sostituendo i valori: , , . Conversione della Scala in mm: Dato che equivale a , calcoliamo la conversione in mm/pixel: . Quindi, ogni pixel nella figura corrisponde a circa . Esempio di Applicazione: Conversione Distanza in mm Se , allora: .
Calcolo della distanzaCalcolo della Distanza tra i Punti Le coordinate dei punti sono: e . La formula per la distanza euclidea è: . Sostituendo i valori: , , . Conversione della Scala in mm: Dato che equivale a , calcoliamo la conversione in mm/pixel: . Quindi, ogni pixel nella figura corrisponde a circa . Esempio di Applicazione: Conversione Distanza in mm Se , allora: .
Fattore di scala utilizzato: ![]() Distanze condilariCalcolo delle distanze tra i punti Le coordinate dei punti estrapolate da Geogebra dopo calibrazione, per il condilo laterotrusivo, sono: 1L: , 2L: , 3L: , 4L: , 5L: , 6L: , 7L: , 8L: . Fattore di scala: . Distanze rispetto a : , . : , . : , . : , . : , . : , . : , .
Distanze condilariCalcolo delle distanze tra i punti Le coordinate dei punti estrapolate da Geogebra dopo calibrazione, per il condilo laterotrusivo, sono: 1L: , 2L: , 3L: , 4L: , 5L: , 6L: , 7L: , 8L: . Fattore di scala: . Distanze rispetto a : , . : , . : , . : , . : , . : , . : , .
- 1 cm = 10 mm = 239.02 pixel**
- Scala in mm/pixel:**
| Punti | Coordinate (x, y) | Distanza (pixel) | Distanza (mm) |
|---|---|---|---|
| 1L → 2L | (58.3, -50.9) → (59, -92.3) | 41.41 px | 1.734 mm |
| 1L → 3L | (58.3, -50.9) → (46.3, -169.5) | 119.17 px | 4.99 mm |
| 1L → 4L | (58.3, -50.9) → (44.1, -207.7) | 157.43 px | 6.59 mm |
Movimenti Condilari: Traslazioni e Rotazioni
Vettore di Posizione del Condilo Laterotrusivo
Il condilo laterotrusivo (lato del movimento) è descritto dal vettore:
Dove:
- : spostamenti lineari.
- : rotazioni sugli assi cartesiani, secondo gli **angoli di Eulero**.
Vettore di Traslazione del Condilo Mediotrusivo
Il condilo mediotrusivo segue una **traslazione antero-mediale**, descritta dal vettore:
Conclusioni
L’analisi della cinematica mandibolare a **sei gradi di libertà** permette di ottenere dati affidabili per applicazioni cliniche e protesiche. Nei capitoli successivi approfondiremo questi argomenti non banali.
- ↑ Curtis, D.A. & Sorensen, J.A. Errors incurred in programming a fully adjustable articulator with a pantograph. J Prosthet Dent. 1986; 55:427-429.
- ↑ Cite error: Invalid
<ref>tag; no text was provided for refs named:0 - ↑ Cite error: Invalid
<ref>tag; no text was provided for refs named:1 - ↑ Payne, J. Condylar determinants in a patient population: electronic pantograph assessment. J Oral Rehabil. 1997; 24:157-163.
- ↑ Bennett, N.G. A contribution to the study of the movements of the mandible. Proc R Soc Med. 1908; 1:79-98.
- ↑ Taylor, T.D., Bidra, A.S., Nazarova, E. Clinical significance of immediate mandibular lateral translation: A systematic review. J Prosthet Dent. 2016; 115:412-418.
- ↑ Cite error: Invalid
<ref>tag; no text was provided for refs named:2




















































![{\displaystyle P_{l}(t)=[X_{l}(t),Y_{l}(t),Z_{l}(t),\theta _{l}(t),\phi _{l}(t),\psi _{l}(t)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0460bad60fdbd2bf924fac810d7383a682d79d9e)


