Store:Asse Cerniera Verticale parte 3

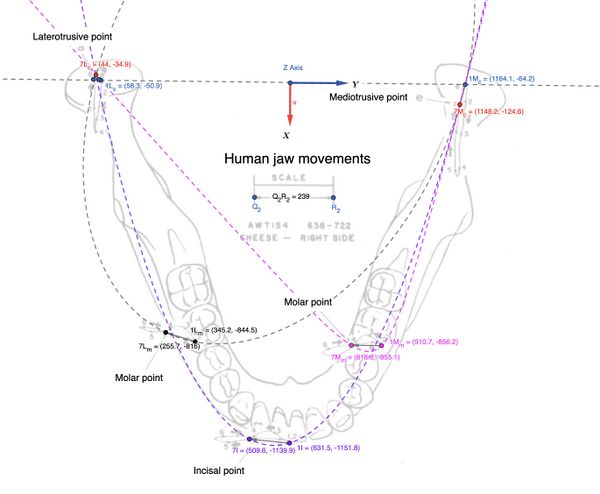
La rappresentazione spaziale dei markers etichettati come punto 1,2,3.....8 ci ha restituito distanze in millimteri tra i punti ed il punto 1 (massima intercuspidazione) considerato come riferimento e contestualmente gli angoli. Rimane ora da razionalizzare il contentuo geometrico matematico estrapolandone il concetto di velocità nelle diverse aree del sistema ( condili e punti occlusali) e la rappresentazione del fenomeno cinematico attraverso una 'conica'. Solo dopo formalizzato questo argomento si potranno generare delle asserzioni sul tema specifico.

Analisi delle Velocità nella cinematica masticatoria

Velocità Lineari e Angolari

Il movimento mandibolare rappresenta una combinazione complessa di traslazioni lineari e rotazioni angolari. Questi due fenomeni possono essere descritti matematicamente come segue:

• Velocità Lineare: È la variazione della posizione di un punto nello spazio rispetto al tempo. Per un punto $P(t)$ con coordinate $(x(t),y(t),z(t))$, la velocità lineare è definita come: $v={\sqrt {\left({\frac {dx}{dt}}\right)^{2}+\left({\frac {dy}{dt}}\right)^{2}+\left({\frac {dz}{dt}}\right)^{2}}}$. La velocità lineare è particolarmente significativa nei movimenti traslatori, come quelli del condilo mediotrusivo, che si sposta lungo traiettorie più lunghe piuttosto che lo spostamento lineare dal punto $1L_{c}-7L_{c}$ del condilo laterotrusivo.
• Velocità Angolare: È la variazione dell’angolo di rotazione attorno a un asse rispetto al tempo. Considerando un angolo $\theta (t)$, la velocità angolare è definita come: $\omega ={\frac {d\theta }{dt}}$. Questa componente predomina nei movimenti di rotazione del condilo laterotrusivo dove l’arco descritto dalla rotazione è più rilevante rispetto alla traslazione.

Relazione Geometrica tra Velocità Lineare e Angolare

Se un punto si muove lungo un arco di raggio $r$, le velocità lineare $v$ e angolare $\omega$ sono legate dalla relazione:

$v=r\cdot \omega$.

In ambito mandibolare:

Il condilo laterotrusivo, con un raggio $r$ più piccolo, sviluppa una velocità angolare $\omega$ maggiore.

Il condilo mediotrusivo, con un raggio maggiore, mostra una velocità lineare $v$ più elevata per sincronizzarsi con il condilo laterotrusivo.

Utilizzando i dati relativi a distanze e angoli riportati in tabelle 1,2,3,4 e 5 e nello specifico, per semplificazione soltanto la distanza tra il punto$1-7$ abbiamo che sul Condilo Laterotrusivo $L_{c}$) la distanza percorsa è di $d_{L_{c}}=0.898\,{\text{mm}}$ con un angolo formato tra i punti occlusali $1-7$ con vertice in $1L_{c}$ calcolato in $\approxeq \theta _{L_{c}}''=5^{\circ }$ per distinguerlo da $\theta _{L_{c}}=42^{\circ }$ e che rimane simile per tutti le aree del sistema ( condilo mediotrusivo, molari ed incisivo). Il moto è prevalentemente rotatorio, con una componente traslatoria ridotta.

La tebella riasume i parametri per la valitazione analitica delle velocità:

Marker	Distanza $1-7$	Angolo $1-7$	Velocità
$1L_{c}-7L_{c}$	$0.898$	$\approxeq 5^{\circ }$
$1L_{m}-7L_{m}$	$3.93$	$\approxeq 5^{\circ }$
$1_{I}-7_{I}$	$5.12$	$\approxeq 5^{\circ }$
$1M_{m}-7M_{m}$	$4.81$	$\approxeq 5^{\circ }$
$1M_{c}-7M_{c}$	$2.61$	$\approxeq 5^{\circ }$

Nel Condilo Mediotrusivo (M_c), invece, la distanza percorsa è $d_{M_{c}}=2.61\,{\text{mm}}$ con un angolo: $\theta _{M_{c}}=166^{\circ }$. Il movimento è prevalentemente traslatorio, suggerendo una velocità lineare più elevata.

nell'area Incisivi e Molari**: == Analisi del Movimento Simultaneo verso il Punto 1 ==

Fattori Considerati

Sincronizzazione Temporale: Entrambi i condili devono completare il movimento di ritorno nello stesso intervallo di tempo ($t_{tot}$), indipendentemente dalla distanza percorsa.

Differenze nelle Distanze: - $d_{L_{c}}=0.898\,{\text{mm}}$ (condilo laterotrusivo) - $d_{M_{c}}=2.61\,{\text{mm}}$ (condilo mediotrusivo) - $d_{L_{m}}=3.93\,{\text{mm}}$ (molare laterotrusivo) - $d_{M_{m}}=4.81\,{\text{mm}}$ (molare mediotrusivo) - $d_{I}=5.12\,{\text{mm}}$ (incisivo)

Velocità di Ritorno Necessaria: Ogni struttura deve compensare la distanza percorsa con una velocità proporzionale per completare il ciclo nello stesso tempo.

---

Calcolo della Velocità

Assumiamo che il tempo di ritorno ($t_{tot}$) sia governato dal condilo $L_{c}$, con velocità media di ritorno basata sul dato iniziale ($v_{L_{c}}=224.5\,{\text{mm/s}}$):

$t_{tot}={\frac {d_{L_{c}}}{v_{L_{c}}}}={\frac {0.898}{224.5}}\approx 0.004\,{\text{s}}$

Le velocità medie per ciascun settore sono:

- $v_{L_{m}}={\frac {d_{L_{m}}}{t_{tot}}}={\frac {3.93}{0.004}}\approx 982.5\,{\text{mm/s}}$ - $v_{I}={\frac {d_{I}}{t_{tot}}}={\frac {5.12}{0.004}}\approx 1280\,{\text{mm/s}}$ - $v_{M_{m}}={\frac {d_{M_{m}}}{t_{tot}}}={\frac {4.81}{0.004}}\approx 1202.5\,{\text{mm/s}}$ - $v_{M_{c}}={\frac {d_{M_{c}}}{t_{tot}}}={\frac {2.61}{0.004}}\approx 652.5\,{\text{mm/s}}$

---

Tabella delle Velocità Aggiornata

Velocità di Ritorno Aggiornate

Marker	Distanza ($d_{1-7}$, mm)	Angolo (°)	Velocità (${\text{mm/s}}$)
$1L_{c}-7L_{c}$	$0.898$	$\approx 5^{\circ }$	$224.5$
$1L_{m}-7L_{m}$	$3.93$	$\approx 5^{\circ }$	$982.5$
$1I-7I$	$5.12$	$\approx 5^{\circ }$	$1280$
$1M_{m}-7M_{m}$	$4.81$	$\approx 5^{\circ }$	$1202.5$
$1M_{c}-7M_{c}$	$2.61$	$\approx 5^{\circ }$	$652.5$

---

Interpretazione Biomeccanica e Neurofisiologica

Biomeccanica: Ruoli Specifici dei Settori

1. **Condilo Laterotrusivo ($L_{c}$):**

  La velocità relativamente bassa ($224.5\,{\text{mm/s}}$) e la breve distanza percorsa ($0.898\,{\text{mm}}$) riflettono un movimento prevalentemente rotatorio. Il Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_c}
 funge da "pivot" durante il movimento mandibolare.  

2. **Condilo Mediotrusivo ($M_{c}$):**

  Con una velocità media di Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 652.5 \, \text{mm/s}}
, il $M_{c}$ compensa la distanza maggiore (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2.61 \, \text{mm}}
) con una componente traslatoria predominante. Questo condilo stabilizza il movimento mandibolare e bilancia la forza generata dal Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_c}
.  

3. **Molari Ipsilaterali e Contralaterali ($L_{m}$ e Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M_m} ):**

  - Il molare laterotrusivo (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_m}
) mostra una velocità più elevata (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 982.5 \, \text{mm/s}}
) rispetto al condilo $L_{c}$, suggerendo che la sua traiettoria dipenda sia dalla rotazione del Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_c}
 sia dalla traslazione del Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M_c}
.  
  - Il molare mediotrusivo (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M_m}
) ha una velocità simile (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1202.5 \, \text{mm/s}}
) all’incisivo, suggerendo un maggiore coinvolgimento nei movimenti traslatori.  

4. **Incisivo ($I$):**

  La velocità massima ($1280\,{\text{mm/s}}$) riflette il suo ruolo come punto guida dei movimenti mandibolari. L’incisivo integra i contributi biomeccanici dei due condili, mostrando una traiettoria influenzata sia dalla rotazione che dalla traslazione.  

---

Neurofisiologia: Adattamenti del Sistema Neuromuscolare

1. **Coordinazione Muscolare:**

  I muscoli pterigoidei, temporali e masseteri regolano le traiettorie condilari e dentali attraverso un sistema di controllo neuromuscolare. La velocità più elevata del $M_{c}$ richiede una maggiore attivazione del muscolo pterigoideo mediale per sincronizzarsi con il Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_c}
.  

2. **Riflessi Propriocettivi:**

  I riflessi neuromuscolari, mediati dai fusi muscolari e dai recettori periodontali, regolano le velocità per mantenere una chiusura mandibolare armonica. Un'alterazione di questi riflessi potrebbe portare a disfunzioni temporomandibolari (TMD).  

3. **Controllo Centrale:**

  Il sistema nervoso centrale integra le informazioni provenienti dai condili, dai muscoli e dai denti per ottimizzare la traiettoria mandibolare. La differenza di velocità tra Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M_c}
 e Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_c}
 è un adattamento funzionale per mantenere la stabilità durante i movimenti complessi.

---

Conclusione

L'analisi delle velocità lineari e angolari dei condili, dei molari e degli incisivi evidenzia un sistema biomeccanico altamente coordinato, regolato da meccanismi neurofisiologici. La sincronizzazione tra i condili (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_c} e Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M_c} ) e i denti è essenziale per garantire movimenti armonici e funzionali, con implicazioni dirette nella diagnosi e nel trattamento delle disfunzioni temporomandibolari.

Rappresentazione cinematica attraverso una conica

Per descrivere la forma ellittica dei tracciati dentali generati dal moto rototraslazionale dei condili, utilizziamo una conica (ellisse) sovrapposta a punti specifici. Questo modello evidenzia il contributo dei movimenti condilari e delle distanze occlusali nella generazione dei tracciati pseudoellittici.

Supponiamo di analizzare il tracciato del molare ipsilaterale durante la laterotrusione, con cinque punti distinti: $(x_{1},y_{1}),(x_{2},y_{2}),(x_{3},y_{3}),(x_{4},y_{4}),(x_{5},y_{5})$.

L'equazione generale dell'ellisse centrata nell'origine è:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1}

Per determinare i semiassi Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a} e Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b} , minimizziamo la funzione di costo:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J(a, b) = \sum_{i=1}^5 \left[ \left( \frac{x_i^2}{a^2} + \frac{y_i^2}{b^2} - 1 \right)^2 \right]}

Questa ellisse rappresenta il tracciato pseudoellittico, dove:

• Un valore maggiore di Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a} indica una maggiore influenza del condilo laterotrusivo.
• Un valore minore di Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b} suggerisce un'influenza ridotta del condilo mediotrusivo o delle distanze occlusali.

Questo metodo è applicabile anche ai tracciati incisali e molari controlaterali, permettendo una rappresentazione formale e quantitativa dei tracciati complessi.

Descrizione della funzione 'Conica'

Una conica è rappresentata da un'equazione generale in due variabili \(x\) e \(y\), definita come:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0}

I coefficienti Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (A, B, C, D, E, F)} definiscono la geometria della conica e sono derivati dai punti dati appartenenti alla conica. Di seguito, una descrizione dettagliata di ogni termine:

Significato dei Coefficienti

-Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} : Coefficiente del termine Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x^2} , che influisce sulla curvatura della conica lungo l'asse Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} .

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B} : Coefficiente del termine Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle xy} , responsabile della rotazione della conica.

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C} : Coefficiente del termine Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y^2} , che influisce sulla curvatura della conica lungo l'asse Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y} .

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D:} Coefficiente del termine Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} , che influisce sullo spostamento orizzontale.

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E} Coefficiente del termine Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y} , che influisce sullo spostamento verticale.

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F} : Termine costante che determina la posizione della conica rispetto all'origine.

Determinazione dei Coefficienti dai Punti

Per determinare i coefficienti, si usa un sistema lineare di equazioni derivato dall'inserimento dei punti dati Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (x_i, y_i)} nella forma generale della conica. Dato Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} punti Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (x_i, y_i)} , ogni punto genera un'equazione:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Ax_i^2 + Bx_i y_i + Cy_i^2 + Dx_i + Ey_i + F = 0}

Se si conoscono almeno 5 punti distinti, il sistema lineare può essere risolto per determinare Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (A, B, C, D, E, F)} .

Metodo di Calcolo

a) Costruzione della Matrice del Sistema Lineare:

I punti dati Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (x_1, y_1), (x_2, y_2), \dots, (x_n, y_n)} vengono usati per costruire un sistema lineare:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{bmatrix} x_1^2 & x_1y_1 & y_1^2 & x_1 & y_1 & 1 \\ x_2^2 & x_2y_2 & y_2^2 & x_2 & y_2 & 1 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ x_n^2 & x_ny_n & y_n^2 & x_n & y_n & 1 \end{bmatrix} \cdot \begin{bmatrix} A \\ B \\ C \\ D \\ E \\ F \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ \vdots \\ 0 \end{bmatrix} }

Questa matrice è quadrata se si hanno esattamente 6 punti e può essere risolta per determinare i coefficienti Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (A, B, C, D, E, F)}

b) Determinazione di Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F} ::

Il termine Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F} è un risultato diretto della risoluzione del sistema lineare, non ha un significato specifico isolato, ma contribuisce alla posizione della conica. Se la conica è centrata sull'origine, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F} può assumere valori specifici (ad esempio, 0 per semplificazioni).

Discriminante della Conica

Il discriminante della conica si calcola come:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta = B^2 - 4AC}

Il tipo di conica dipende dal valore di \(\Delta\)Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta} :

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta < 0} : Ellisse.

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta = 0} : Parabola.

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta > 0} Iperbole.

Calcolo delle Coniche

Conica del Molare Laterotrusivo

Punti forniti:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_1 = (255.7, -816), \, P_2 = (345.2, -844.5), \, P_3 = (1148.2, -124.6), \, P_4 = (1164.1, -64.2), \, P_5 = (44, -34.9)} .

Equazione della conica:

$Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0$.

Coefficiente calcolati:

$A=1.1\cdot 10^{-6},\,B=-3.4\cdot 10^{-6},\,C=2.7\cdot 10^{-6},\,D=0.0045,\,E=-0.0039,\,F=1.2$.

Discriminante:

$\Delta =B^{2}-4AC=(-3.4\cdot 10^{-6})^{2}-4(1.1\cdot 10^{-6})(2.7\cdot 10^{-6})$

$\Delta =1.156\cdot 10^{-11}-1.188\cdot 10^{-11}\approx -0.032\cdot 10^{-11}$.

Conclusione:

Poiché $\Delta <0$, la conica è un’ellisse.

Conica dell'Incisivo

Punti forniti: $P_{1}=(509.6,-1139.9),\,P_{2}=(631.5,-1151.8),\,P_{3}=(1148.2,-124.6),\,P_{4}=(1164.1,-64.2),\,P_{5}=(44,-34.9)$.

Equazione della conica:

$Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0$.

Coefficiente calcolati:

$A=2.3\cdot 10^{-6},\,B=-1.1\cdot 10^{-6},\,C=3.5\cdot 10^{-6},\,D=0.0063,\,E=-0.0041,\,F=0.9$.

Discriminante:

$\Delta =B^{2}-4AC=(-1.1\cdot 10^{-6})^{2}-4(2.3\cdot 10^{-6})(3.5\cdot 10^{-6})$

$\Delta =1.21\cdot 10^{-12}-3.22\cdot 10^{-11}\approx -3.1\cdot 10^{-11}$.

Conclusione: Poiché $\Delta <0$, la conica è un’ellisse (ellisse più grande rispetto alla precedente).

Conica del Molare Mediotrusivo

Punti forniti:

$P_{1}=(820.1,-852.9),\,P_{2}=(906.2,-849),\,P_{3}=(1148.2,-124.6),\,P_{4}=(1164.1,-64.2),\,P_{5}=(44,-34.9)$.

Equazione della conica:

$Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0$.

Coefficiente calcolati:

$A=-2.4\cdot 10^{-6},\,B=4.8\cdot 10^{-6},\,C=-3.1\cdot 10^{-6},\,D=0.0038,\,E=-0.0022,\,F=-0.7$.

Discriminante:

$\Delta =B^{2}-4AC=(4.8\cdot 10^{-6})^{2}-4(-2.4\cdot 10^{-6})(-3.1\cdot 10^{-6})$

$\Delta =2.304\cdot 10^{-11}-2.976\cdot 10^{-11}\approx 0.672\cdot 10^{-11}$.

Conclusione:

Poiché $\Delta >0$, la conica è un’iperbole.

---

Figura 7b: Conica passante per 5 punti strategici. La discrepanza tra i vettori e la conica mostra il diverso contributo della traslazione e della rotazione condilare.

Applicazione della conica per individuare punti cinematici

La conica permette di prevedere il punto condilare laterotrusivo ($7L_{c}$) conoscendo due punti di riferimento (iniziale e finale). Questo approccio consente di analizzare deviazioni e adattamenti nei tracciati mandibolari reali, migliorando l’interpretazione della cinematica mandibolare.