Logik der medizinischen Sprache: Einführung in die quantenähnliche Wahrscheinlichkeit im Kausystem
Change language
[[|German]]
[[|Spanish]]
[[|French]]
[[|Italian]]Logik der medizinischen Sprache: Einführung in die quantenähnliche Wahrscheinlichkeit im Kausystem
Zusammenfassung
Manchmal denken wir: „Kann die tiefgreifende Realität eines Systemzustands nur auf eine makroskopische Beobachtung (Observable) reduziert werden, wenn ein solch komplexes System eine Menge gemischter Zustände ist? Darüber hinaus hat das Teilen einer Interpretation von „Normokklusion oder Malokklusion“ durch eine klassische statistische Beschreibung nichts mit einer Quanteninterpretation der Realität zu tun, da wir in der klassischen makroskopischen Phänomene (Unterkieferbewegungen, Kiefergelenk usw.) beobachten, während wir in Wirklichkeit quantenhaft sind befassen sich mit mesoskopischen Phänomenen wie synaptischen Übertragungen.
Könnte diese deterministische (Ursache / Wirkung) Mentalität in ein formales Modell umgewandelt werden, das Quantenmathematik verwendet und in der Lage wäre, die mesoskopische stochastische Dynamik des Kausystems zu untersuchen? Wir werden versuchen, dieses Thema zu vertiefen, das nur scheinbar kritisierbar ist, aber im Grunde alles von der Unfähigkeit abhängt, geistige Veränderungen zu akzeptieren.
Einführung
Zum zweiten Mal sehen wir uns einer erkenntnistheoretischen Untersuchung eines Themas gegenüber, auf dem die meisten zahnärztlichen Rehabilitationsdisziplinen basieren, dem der „Malokklusion“, das im Lichte dessen, was in den vorangegangenen Kapiteln gesagt wurde, eine Klärung verdient.
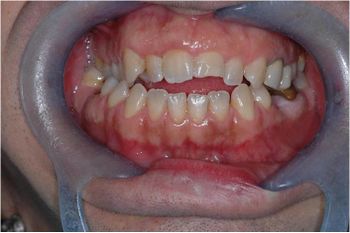
Im ersten Kapitel „Einführung“ haben wir bereits den Patienten in Abbildung 1 erwähnt, bei dem es gegenüber der kieferorthopädischen Disziplin respektlos wäre, einen Zustand der „Malokklusion“ nicht zu berücksichtigen, aber wir haben in gewisser Weise auch die „Axiomatische Information“ durch Ersetzen in Frage gestellt das klassische kieferorthopädische Dogma mit einer neurophysiologischen Sicht auf den Systemzustand des Patienten. Aus diesem Ansatz wurde deutlich, dass sich die mesoskopische Realität stark von der makroskopischen Realität unterscheidet, an die wir gewöhnt sind.
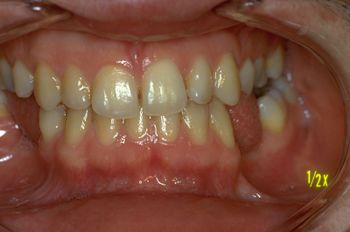
Aber wenn dies eine Anomalie ist, was können wir dann von dem Patienten in Abbildung 2 erwarten, der sich einer orthognathen Operation unterzieht (lesen Sie die beschreibende Bildunterschrift) ?
Abbildung 1: Patient Nr. 1 mit offenem Biss und rechtem posteriorem Kreuzbiss, was kieferorthopädisch als „Malokklusion“ gilt.
Abbildung 1: Patient Nr. 2 nach einer orthognathen chirurgischen Therapie für eine III-Skelettklasse. Die Wiederherstellung der „normalen Okklusion“ ist zumindest in Bezug auf das okklusale Bild von Patient Nr. 1 formal optimal. Abgesehen von einer leichten Abweichung der inzisalen Mittellinie und der partiellen Unterkieferzahnlosigkeit berichtet die Patientin zur großen Zufriedenheit der MKG-Chirurgen von einer bemerkenswerten ästhetischen Zufriedenheit und einer scheinbar guten Kaufunktion.
Der orthognathe Chirurgie behandelte Patient (Abb. 2), der elektrophysiologischen Trigeminusuntersuchungen unterzogen wurde, zeigte ein äußerst ernstes Bild des „Systemzustands“ mit ausgeprägten Asymmetrien der Trigeminusreflexe, um eine neurophysiopathologische Untersuchung einzuleiten. Diese Daten weisen auf eine „Malokklusion“ hin, auch wenn die intermaxillären Beziehungen okklusal objektiv in einem viel kongruenteren Zustand erscheinen als bei Patient Nr. 1 in Abbildung 1.
Nachdem dies gesagt wurde, macht es uns nachdenklich:
„Kann die tiefgreifende Realität eines ‚Systemzustands‘ nur auf eine makroskopische Beobachtung (Observable) reduziert werden, wenn ein solches ‚komplexes System‘ eine Menge gemischter Zustände ist? Darüber hinaus hat das Teilen einer Interpretation von „Normokklusion oder Malokklusion“ durch eine klassische statistische Beschreibung nichts mit einer Quanteninterpretation der Realität zu tun, da wir in der klassischen makroskopischen Phänomene (Unterkieferbewegungen, Kiefergelenk usw.) beobachten, während wir in Wirklichkeit quantenhaft sind befassen sich mit mesoskopischen Phänomenen wie synaptischen Übertragungen.
Hier kommt ein sehr extravagantes und riskantes, aber kontextbedeutsames Argument, was in der Quantenphysik Superposition von Zuständen in einem „System“ genannt wird.
(Natürlich werde ich Sie sofort zufrieden stellen, indem ich das Paradox von Schrödingers Katze erkläre)
Schrödingers Katze
Die "Philosophie" der Überlagerung von Quantenzuständen
Nel 1935 Erwin Schrödinger:[1][2] Um die paradoxen Ergebnisse der Kopenhagener Interpretation hervorzuheben, schlug er ein imaginäres Experiment vor, bei dem eine Katze in eine Kiste gesetzt wird, die eine mit Gift verschlossene Phiole enthält. Dank eines gut konstruierten Mechanismus könnte das Fläschchen zerbrechen. Abbildung 3 stellt das soeben freigelegte imaginäre Gerät grafisch dar. Um die Bedeutung dieses Verweises auf Quanten besser zu verstehen, berichten wir über einen bestimmten Inhalt, der aus Wikipedia extrahiert wurde.[3]
Eine Katze ist zusammen mit folgender Höllenmaschine (die davor geschützt werden muss, direkt von der Katze gepackt zu werden) in einer Stahlkiste eingesperrt: In einem Geigerzähler befindet sich eine winzige Portion radioaktiver Substanz, so wenig, dass in der Im Laufe von a zerfällt jetzt vielleicht eines seiner Atome, aber ebenso wahrscheinlich auch keines; Wenn das Ereignis eintritt, signalisiert der Zähler dies und aktiviert ein Relais eines Hammers, der ein Fläschchen mit Zyanid zerbricht. Nachdem man dieses ganze System eine Stunde ungestört gelassen hat, scheint die Katze noch am Leben zu sein, wenn in der Zwischenzeit kein Atom zerfallen wäre, während der erste Atomzerfall sie vergiftet hätte.
Die mathematische Funktion Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi} des ganzen Systems führt zu der Behauptung, dass in ihm die lebende Katze und die tote Katze keine reinen Zustände sind, sondern gleichgewichtig vermischt.[4]
(Ich bin gespannt, wo du hin willst)
Oft wird das Ergebnis des Experiments in den folgenden Begriffen dargestellt. Nach einem Intervall, das der Halbwertszeit entspricht, kann das Atom mit der gleichen Wahrscheinlichkeit zerfallen sein oder nicht, so dass es sich in einer Überlagerung der beiden Zustände befindet: In der Dirac-Notation ist der Zustand des Atoms:
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |A \rangle = \frac{1}{\sqrt{2}} \, \left( | \textrm{verfallen } \rangle + | \textrm{nein} \; \textrm{ verfallen} \rangle \right) }
Wir fangen an, Begriffe der Quantenmathematik zu verwenden, in der Tat das Akronym Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |A \rangle } steht für "ket"[5]
Da aber der Verfall über das Schicksal der Katze entscheidet, sollte sie sowohl als lebendig als auch als tot betrachtet werden:
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |G \rangle = \frac{1}{\sqrt{2}} \, \left( | \textrm{tot} \rangle + | \textrm{Ich wohne} \rangle \right) }
zumindest bis eine direkte Beobachtung durch Öffnen der Box erfolgt. Dabei ist zu bedenken, dass die direkte Beobachtung aus einem Beobachter und einem Messmittel besteht.
Das scheinbare Paradox ergibt sich aus der Tatsache, dass es in der Quantenmechanik nicht möglich ist, Objekte klassisch zu beschreiben, und eine probabilistische Darstellung verwendet wird: Um zu zeigen, dass ein Teilchen beispielsweise an verschiedenen Orten platziert werden kann, wird es so beschrieben, als ob es waren gleichzeitig in allen Positionen, die es einnehmen kann. Jeder möglichen Position entspricht die Wahrscheinlichkeit, dass sich das Teilchen bei Beobachtung an dieser Position befindet. Die Beobachtungsoperation modifiziert das System jedoch unwiederbringlich, da das Teilchen, wenn es einmal an einer Position beobachtet wurde, diese Position definitiv einnimmt (dh es hat die Wahrscheinlichkeit 1, dort zu sein) und sich daher nicht mehr in einer "Überlagerung von Zuständen" befindet.
Um auf den Fall der Katze zurückzukommen, sollte jedoch angemerkt werden, dass die obige Beschreibung falsch ist.[6] Dieselbe Schlussfolgerung von Schrödinger, der den Begriff „Paradoxon“ dennoch nie verwendet, wird in ganz anderen Worten ausgedrückt: Schrödinger bezieht sich auf die Wellenfunktion des Gesamtsystems, nicht auf die der Katze. Tatsächlich besagt die Quantentheorie, dass das System Atom + Katze durch den Quantenkorrelationszustand beschrieben wird.
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |A, G \rangle = \frac{1}{\sqrt{2}} \, \left( | \textrm{Atom } \; \textrm{verfallen, } \; \textrm{Katze} \; \textrm{tot} \rangle + | \textrm{atom} \; \textrm{nicht} \; \textrm{verfallenes,} \; \textrm{Katze} \; \textrm{leben} \rangle \right). }
Es ist daher nicht richtig zu sagen, dass sich die Katze in einer Überlagerung zweier Zustände befindet, da die Überlagerung das gesamte System betrifft.[7] Der grundlegende Unterschied besteht darin, dass die beiden Teilsysteme, also das Atom und die Katze einzeln genommen, eher durch eine statistische Mischung beschrieben werden.[8] Die Ungewissheit über das Schicksal der Katze ist „klassisch“: Sie ist mit einer Wahrscheinlichkeit von 50 % lebendig oder tot, ohne dass es zu einer Interferenz zwischen den beiden unterschiedlichen Zuständen kommt.
Die von Schrödinger zum Ausdruck gebrachte Ratlosigkeit liegt darin, dass die Quantenmechanik offenbar auch auf ein Lebewesen anwendbar ist, das sich in einem Zustand der Quantenkorrelation ( Verschränkung ) mit einem Teilchen befinden kann. Es ist daher legitim zu fragen, ob auch ein makroskopisches Objekt den Gesetzen der Quantenmechanik gehorchen sollte, ohne die Möglichkeit, seine Wirkungen auf experimenteller Ebene zu überprüfen.
Schrödinger beschrieb die zuvor beschriebene teuflische Vorrichtung, durch die sich eine Katze mit einem einzelnen Atom verheddern würde. Das System würde durch eine Wellenfunktion beschrieben, die üblicherweise mit Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi} abgekürzt wird und gleichzeitig die lebende Katze mit dem angeregten Atom und die tote Katze mit dem Atom darstellt, das in den Grundzustand zurückkehrt, nachdem sein Zerfall das tödliche Gerät ausgelöst hat . Experten der Quantenphysik werden einwenden, dass die Katze ein offenes komplexes System ist, das selbst zu Beginn des grausamen Experiments nicht durch eine Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi} Wellen-Funktion beschrieben werden kann. Die Argumentation wirft jedoch eine wichtige Frage auf: Warum und wie verschwindet die Verrücktheit der Quantenwelt in makroskopischen Systemen?[9]
Die Besonderheit besteht darin, dass das Zerbrechen des Fläschchens durch den Zerfall von Teilchen bestimmt wird (Prozess unterliegt Quantenregeln). Quantenregeln (mikroskopische Teilchen) unterscheiden sich stark von denen der makroskopischen Physik: Mit diesem Gedankenexperiment war es jedoch möglich, das Leben der Katze durch Quantenregeln zu konditionieren.
Es ist interessant zu sehen, wie Schrödinger es geschafft hat, mit einem imaginären Experiment die Konsequenzen der Quantentheorie in die makroskopische Welt einzubeziehen, die von der Katze repräsentiert wird.
Der mathematische Formalismus
Das Katzenexperiment hängt, wie erwähnt, mit dem Problem der Messung zusammen. Ein Quantensystem befindet sich in einer Überlagerung zweier Zustände Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} Und Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B} (mathematisch dargestellt durch das 'ket' Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |A\rangle+|B\rangle} ); eine Beobachtung davon zwingt das System, endgültig oder in die Zukunft zu gehen Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |A\rangle} oder im Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |B\rangle} . Durch die Anwesenheit der Katze wird die Überlagerung, in der sich das Atom befindet, in das Gesamtsystem (Atom + Katze) „übertragen“. Das Atom befindet sich daher nicht mehr in einer Überlagerung, genauso wenig wie die Katze. Aus dieser ersten Darstellung verstehen wir die Bedeutung des Arguments
Die einzige Möglichkeit, den Zustand der Katze zu verstehen, besteht darin, die Schachtel zu öffnen und zu prüfen, ob die Zyanid-Ampulle zerbrochen und die Katze folglich tot ist.
Die Formel, die diese Situation darstellt, lautet wie folgt:
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi(t_0)=|1\rangle |live\rangle} was folgendermaßen gelesen werden kann: Die Wellenfunktion Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi} über der Zeit Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t_0} ist die gleiche wie ket Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |1\rangle} und die Katze lebt
Ein Zustand, der sich dann in einem Zeitraum Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T } entwickeln wird, in dem (abgesehen von Phasen- und Normierungsfaktoren) die beiden Zustände in Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t_1} (aufgrund der Unwissenheit des Beobachters?) koexistieren:
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi(t_1)=|1\rangle |live \rangle + |0\rangle |tot\rangle}
Was wird Zustand zusammenbrechen Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi(t_1)=|1\rangle |live\rangle + |0\rangle |dead\rangle} in eins Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |1\rangle |live\rangle} oder nur Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |0\rangle |dead\rangle} ?
Abgesehen von den verschiedenen Interpretationen wird der Kollaps nach orthodoxer Auffassung durch die Wechselwirkung mit einem makroskopischen Messobjekt verursacht, dh wenn dieses „Observable“ vom Beobachter beobachtet wird. Wir haben daher ein (beobachtbares) System erzeugt, das aus dem physikalischen Zustand des Systems selbst, einem Beobachter und einem Messinstrument besteht.
Um genau zu sein, die Formel Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi(t_1)=|1\rangle |live \rangle + |0\rangle |tot\rangle} ist unvollständig, Sie müssen jeden Term rechts von der Gleichung mit einer Zahl multiplizieren. Die Zahl gibt die „Wahrscheinlichkeit“ an, dass das bestimmte Ereignis eintritt, die vollständige Formel lautet:
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi(t_1)=\sqrt{p_1}|1\rangle |live \rangle + \sqrt{p_0}|0\rangle |tot\rangle}
Die Zahl gibt die Wahrscheinlichkeit (Quadratwurzel) an, dass das bestimmte Ereignis eintritt.
Nehmen wir ein Beispiel, das uns zurück zum medizinischen Bereich bringt:
Wenn das Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |1\rangle |healthy\rangle} -Ereignis eine 50-prozentige Wahrscheinlichkeit hat und das Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |0\rangle |sick \rangle} -Ereignis eine 50-prozentige Wahrscheinlichkeit hat, dann wird die Formel (außer Phasenfaktoren)
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi(t)=\sqrt 50%|1\rangle |gesund \rangle + \sqrt 50%|0\rangle |krank \rangle}
was genauer mathematisch zu wird.
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi(t)=\sqrt 0.5|1\rangle |gesund \rangle + \sqrt 0.5|0\rangle |krank \rangle}
((ja natürlich ist es einfacher als du denkst))
Stellen wir uns vor, dass ein „Observable“ das menschliche Gehirn ist, das rein symbolisch Schrödingers Katzenkiste darstellen könnte, da der Schädel ein Organ von so hervorragender Funktionalität enthält.
An diesem Punkt können wir in Abwesenheit bestimmter Symptome und klinischer Anzeichen sagen, dass die Person gesund ist. In der Praxis haben wir nichts anderes getan, als dasselbe zu sagen, was über Schrödingers Katzenkiste gesagt werden kann, nämlich dass 50 % der Katze leben (gesundes Subjekt) und 50 % tot sein könnten (krankes Subjekt).
Berücksichtigen Sie die Subtilität von Schrödingers Metapher, denn die meisten Menschen schmälern das Konzept, indem sie alles auf eine naive Logik reduzieren, in der die Katze bereits tot war, noch bevor sie die Kiste öffnete, und mein 6-jähriger Neffe hätte diesen Punkt auch erreicht. Schrödinger ist echt Der metaphorische Sinn bezieht sich nicht direkt auf die Katze (makroskopische Struktur), sondern auf das Uranatom (mikroskopische Struktur), das mit einer zufälligen zeitlichen Wahrscheinlichkeit zerfällt (tote Katze), was impliziert, dass das Leben der Katze mit der zeitlich zufälligen Wahrscheinlichkeit des Uranzerfalls verknüpft ist . Kurz gesagt, die Interpretation, die sich aus der makroskopischen Observable ergibt, wäre ein selektiver Filter, der die Interpretation der mikroskopischen Observable verzögert, was bedeutet, dass das Fehlen von Symptomen ein Phänomen sein könnte, das durch den makromolekularen Filter gedämpft wird.
In diesem Sinne ab dem Moment, in dem das Uran nach seinem eigenen zufälligen Zerfallsprozess den Hammer aktiviert, der die Ampulle zerbricht und sich das Zyanid in der Schachtel ausbreitet. Die Zeit, die vom Verfall bis zum tatsächlichen Tod der Katze vergeht Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta(t)} entspricht der Überlagerung von Zuständen.
Wir werden während der Lesungen häufig auf diese Themen zurückkommen, insbesondere bei der Beschreibung der verschiedenen klinischen Fälle, über die berichtet wird, wobei auf die zeitlichen Unterschiede zwischen normalen klinischen Situationen und der Manifestation von Symptomen hingewiesen wird.
Das Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta(t)} ist die Überlagerung von Zuständen und der Kollaps der Wellenfunktion (tote oder lebendige Katze) entspricht einer hauptsächlich quantenmechanischen Dialektik.
Um zu unserem Beispiel zurückzukehren, um zu verstehen, ob das Subjekt tatsächlich, noch besser, das Gehirn des Subjekts intakt oder unstrukturiert ist (der Begriff gesund oder krank ist noch ein weiterer Schritt), sollten wir die Schachtel öffnen und den Zustand des zentralen Nervensystems sehen.
Nicht einmal Schrödinger hätte diese Metapher verwendet, also haben wir Messgeräte erfunden .... fantastisch !!!
(es kommt nicht so sehr darauf an, was es misst, sondern wie das Maß interpretiert wird)
Elektroenzephalographie (EEG)
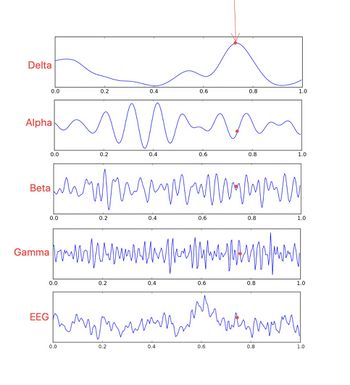
Um beim neurophysiologischen Thema zu bleiben, betrachten wir die EEG-Elektroenzephalographie. Das Messinstrument misst im Grunde nichts anderes als die Differenz des ionischen elektrischen Potentials „Dipol“, der sich mit anhaltender Geschwindigkeit hier und da zwischen den neuralen Verbindungen (Lagrange-Koordinaten) bewegt.[10] Figur 4
Nun, hier führen wir das quantenähnliche Konzept ein: Wenn wir den Zustand des Gehirns durch eine EEG-Messung beobachten, können wir nur sagen, dass der EEG-Zustand in einer solchen Situation nichts anderes ist als eine Überlagerung von gemischten Zuständen, die im Wesentlichen bei sind mindestens die 5 in Abbildung 4 dargestellten Frequenzen der Welle 0Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (\delta,\theta,\alpha,\beta,\gamma)} . (EEG-Spur).
Mit dieser Messung (wenn wir die EEG-Kurve unten in Abbildung 4 betrachten) bleibt es sehr schwierig, den tatsächlichen Integritätszustand eines bestimmten und eingeschränkten Gehirnbereichs zu extrapolieren, selbst unterstützt durch ausgefeilte mathematische / statistische Analysemethoden wie Fourier-Transformationen, Wavelets etc., da die Messunsicherheit mit der gemessenen Volumenamplitude, der neuronalen Entladungsrate, der Abtastfrequenz etc. erheblich zunimmt.
Das EEG ist nicht nur das Ergebnis einer tonischen Aktivität des neuronalen Pools, sondern eine Raum-Zeit-Summe synchroner (phasischer) und asynchroner (tonischer) neuronaler Aktivitäten, die manchmal kollidieren und unter anderem Teile der EEG-Spur auslöschen.
Leider haben wir bei der EEG-Messung eine Form von Unsicherheit der Messdaten. Dieses Phänomen wurde als das analoge Prinzip der "Heisenberg-Unbestimmtheit" der Form definiert, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bigtriangleup x(t)\bigtriangleup p_x(t)\geqq K_{brain}} in welchem Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle K_{brain}} steht für Unsicherheitskonstante der elektroenzephalographischen Messung. Die Autoren dieser Studie[11] fanden heraus, dass ihr quantenähnliches Modell zu einem Mindestwert der Unsicherheitskonstante in führt Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bigtriangleup x(t)\bigtriangleup p_x(t)} und in Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bigtriangleup y(t)\bigtriangleup p_y(t)} von Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0,78\pm0,41 \tfrac{cm^2}{4ms}} beim EEG. (siehe Kapitel 'Exploring electroencephalography with a model inspired by quantum mechanics'.
An diesem Punkt haben wir zwei „Beobachtbare“ bei einem asymptomatischen Subjekt, das rechtzeitig getestet wurde Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t} diejenige, die sich aus der Systemmessung ergibt Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} (EEG), die nach dem Gesagten eine Datensystemintegrität zurückgeben könnte (Daten verschmutzt durch Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle K_{brain}} ) und ein beobachtbares Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B} entsprechend dem Gesundheitszustand des Subjekts, das sich als krank herausstellt.
Die gemäß dieser Projektion beobachtete Realität würde die beiden Observablen machen Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} Und Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B} unvereinbar.
In Lehrbüchern zur Quantenmechanik wird häufig darauf hingewiesen, dass das Hauptunterscheidungsmerkmal der Quantentheorie das Vorhandensein „inkompatibler Observablen“ ist. Erinnern Sie sich, dass zwei Observable, wie in unserem Fall, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} Und Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B} , sind unvereinbar, wenn ihnen keine gemeinsamen Werte zugeschrieben werden können. Im probabilistischen Modell führt dies dazu, dass es unmöglich ist, ihre „Joint Probability“-Verteilung (JPD) zu bestimmen. (siehe Kapitel 'Quantum-like modeling in biology with open quantum systems and instruments')
(.... wir werden in den nächsten Kapiteln sehen, wie sich die Herangehensweise ändert)
- ↑ Milton Packer. The Parable of Schrödinger's Cat and the Illusion of Statistical Significance in Clinical Trials. . Circulation. . 2019 Sep 9;140(10):799-800doi: 10.1161/CIRCULATIONAHA.
- ↑ Carlos E Rochitte. Cardiac MRI and CT: the eyes to visualize coronary arterial disease and their effect on the prognosis explained by the Schrödinger's cat paradox. Radiol Bras..Jan-Feb 2016;49(1):VII-VIII. doi: 10.1590/0100-3984.2016.49.1e2.
- ↑ Schrödinger's cat paradox
- ↑ Schrödinger, Erwin (November 1935). "Die gegenwärtige Situation in der Quantenmechanik (The present situation in quantum mechanics)". Naturwissenschaften. 23 (48): 807–812.
- ↑ Notation bra-ket
- ↑ Stefan Rinner, Ernst Werner: On the role of entanglement in Schrödinger's cat paradox, Central European Journal of Physics 02/2008; 6(1):178-183
- ↑ In fact, the apparatus imagined by Schrödinger is even more complex, because it does not simply include an atom and a cat . To be precise, the other elements, such as the Geiger counter and the cyanide vial, should also be considered, which are also macroscopic. But even with this addition, the conclusions of the reasoning are essentially the same.
- ↑ Scully et al: State reduction in quantum mechanics: a calculational example, Phys. Rep. 43, 485–498 (1978).
- ↑ S. Haroche: Entanglement, decoherence and the quantum/classical boundary Archiviato il 25 aprile 2014 in Internet Archive., Physics Today, July 1998.
- ↑ Bin-Qiang Chen, Bai-Xun Zheng, Chu-Qiao Wang, Wei-Fang Sun. Adaptive Sparse Detector for Suppressing Powerline Component in EEG Measurements. Front Public Health. 2021 May 7;9:669190. doi: 10.3389/fpubh.2021.669190. eCollection 2021.
- ↑ Nicholas J M Popiel, Colin Metrow, Geoffrey Laforge Adrian M Owen, Bobby Stojanoski, Andrea Soddu. Exploring electroencephalography with a model inspired by quantum mechanics. Sci Rep. 2021 Oct 5;11(1):19771. doi: 10.1038/s41598-021-97960-7.