Erforschung der Elektroenzephalographie mit einem von der Quantenmechanik inspirierten Modell

Other languages:

English · Italiano · Français · Deutsch · Español Die Übersetzung dieser Seite ist noch nicht vollständig; schlagen Sie Ihre eigene Übersetzung auf der Diskussionsseite vor.

Free resource

Exploring electroencephalography with a model inspired by quantum mechanics

Free resource by Nicholas J. M. Popiel  · Colin Metrow · Geofrey Laforge  · Adrian M. Owen · Bobby Stojanoski  · Andrea Soddu

Nicholas J. M. Popiel,^1,2 Colin Metrow,¹ Geoffrey Laforge,³ Adrian M. Owen,^3,4,5 Bobby Stojanoski,^#4,6 and Andrea Soddu^{#1,3 1}The Department of Physics and Astronomy, The University of Western Ontario, London, ON N6A 5B7 Canada

²Cavendish Laboratory, University of Cambridge, Cambridge, CB3 0HE UK

³The Brain and Mind Institute, The University of Western Ontario, London, ON N6A 5B7 Canada

⁴The Department of Psychology, The University of Western Ontario, London, ON N6A 5B7 Canada

⁵The Department of Physiology and Pharmacology, The University of Western Ontario, London, ON N6A 5B7 Canada

⁶Faculty of Social Science and Humanities, University of Ontario Institute of Technology, 2000 Simcoe Street North, Oshawa, ON L1H 7K4 Canada

Abstrakt

Ein herausragendes Problem in der kognitiven Neurowissenschaft betrifft die Organisation des Gehirns unter verschiedenen Bedingungen. Zum Beispiel kann das Gehirn während des Ruhezustands in zuverlässige und reproduzierbare Netzwerke geclustert werden (z. B. sensorische, standardmäßige, exekutive Netzwerke). Interessanterweise entstehen dieselben Netzwerke unter aktiven Bedingungen als Reaktion auf verschiedene Aufgaben. Wenn ähnliche Muster neuronaler Aktivität unter verschiedenen Bedingungen gefunden wurden und daher unterschiedliche zugrunde liegende Prozesse und Erfahrungen der Umwelt, ist das Gehirn dann nach einem grundlegenden Organisationsprinzip organisiert? Um dies zu testen, wendeten wir mathematische Formalismen an, die von Quantenmechanismen entlehnt waren, um Daten des Elektroenzephalogramms (EEG) zu modellieren. Wir haben eine Tendenz entdeckt, dass EEG-Signale während der „Ruhe“ in vorderen Regionen des Gehirns lokalisiert und während einer Aufgabe (z. B. beim Ansehen eines Films) gleichmäßiger verteilt sind. Darüber hinaus fanden wir analoge Werte zur Heisenbergschen Unschärferelation, was auf eine gemeinsame zugrunde liegende Architektur der menschlichen Gehirnaktivität unter Ruhe- und Aufgabenbedingungen hindeutet. Diese zugrunde liegende Architektur manifestiert sich in der neuartigen Konstante $K_{brain}$, die mit der geringsten Unsicherheit aus dem Gehirnzustand extrahiert wird. Wir möchten erklären, dass wir die Mathematik der Quantenmechanik verwenden, aber nicht behaupten, dass sich das Gehirn wie ein Quantenobjekt verhält.

Fachbegriffe: Computational Science, Quantenmechanik

Einführung

Ein wichtiges, aber herausragendes Thema in der zeitgenössischen kognitiven Neurowissenschaft ist das Verständnis der organisatorischen Eigenschaften neuronaler Aktivität. Gibt es zum Beispiel eine grundlegende Struktur für die räumlich-zeitlichen Muster der neuronalen Gehirnaktivität unter verschiedenen Bedingungen? Ein gängiger Ansatz zur Beantwortung dieser Frage ist die Untersuchung des Gehirns im „Ruhezustand“. Maßnahmen wie funktionelle Konnektivität, unabhängige Komponentenanalyse und graphentheoretische Metriken wurden auf Daten angewendet, die mit verschiedenen Bildgebungsverfahren (z. B. funktionelle Magnetresonanztomographie (fMRI) und Elektroenzephalographie (EEG)) aufgezeichnet wurden, um Gehirnbereiche zu gruppieren, die ähnliche Aktivitätsmuster aufweisen . Zahlreiche Studien haben gezeigt, dass die Gehirnaktivität während der „Ruhe“ in unterschiedliche Netzwerke gruppiert werden kann; wie sensorische (visuelle und auditive), Standardmodus-, Exekutiv-, Salienz-und Aufmerksamkeitsnetzwerke (ventral und dorsal), die zuverlässig über Tausende von Teilnehmern reproduziert wurden und prädiktiv für phänotypische Maßnahmen wie Kognition und klinische Diagnosen sind. Diese Ergebnisse deuten darauf hin, dass diese Netzwerke ein intrinsischer Aspekt der neuronalen Aktivität sein könnten.

Muster & Mathematik

Tatsächlich wurde der gleiche Satz strukturierter Muster neuronaler Aktivität während "aktiver" Zustände gefunden, beispielsweise während der Erledigung verschiedener Aufgaben.. Zum Beispiel gibt es einen hohen Grad an Übereinstimmung zwischen Netzwerken, die während der Ruhe extrahiert wurden, und denen, die während sensomotorischer Aufgaben extrahiert wurden und kognitive Fähigkeiten auf höherer Ebene (dh Arbeitsgedächtnis)..

Sogar das Erledigen einer so komplizierten Aufgabe wie das Verfolgen der Handlung eines Films ruft die gleiche Netzwerkarchitektur hervor, die im ruhenden Gehirn beobachtet wird. Die Übereinstimmung zwischen aufgaben- und ruhebasierten Netzwerken ist so stark, dass die aufgabenbasierte fMRI-Netzwerkaktivität aus dem Ruhezustand vorhergesagt werden kann, und Rest-Task-Netzwerkpaare können auf individueller Ebene identifiziert werden. Zusammengenommen legen diese Ergebnisse nahe, dass ruhe- und aufgabenbasierte Muster der Gehirnaktivität trotz unterschiedlicher Erfahrungen und kognitiver Prozesse wahrscheinlich eine ähnliche zugrunde liegende neuronale Architektur aufweisen.

Es gibt jedoch wichtige Unterschiede zwischen den Mustern der Gehirnaktivität, die während Ruhezeiten und aufgabenbasierten Paradigmen ausgelöst werden, und den damit verbundenen Erfahrungen und kognitiven Prozessen.

Zum Beispiel wird das Vorhandensein oder Fehlen einer Aufgabe von einer Zunahme der Variabilität über verschiedene Skalen begleitet, einschließlich neuronaler Feuerraten, Änderungen der Feldpotentiale,, Variation im fMRI-Blutsauerstoffspiegel abhängig (FETT-Signal) und im EEG-Frequenzband. Darüber hinaus wurde durch transkranielle Gleichstromstimulation (tDCS) gezeigt, dass die Frontallappenstimulation die Neigung zum Gedankenwandern erhöht.. Wichtig ist, dass diese Unterschiede mit Änderungen in den Eigenschaften der neuralen Aktivität verbunden sind, aber nicht mit Änderungen in der zugrunde liegenden neuralen Architektur.

Gibt es eine Möglichkeit, die gemeinsame neuronale Architektur zu identifizieren, die den kognitiven Prozessen im Zusammenhang mit Ruhe- und Aktivitätszuständen zugrunde liegt, und gleichzeitig zu quantifizieren, wie diese Prozesse von dieser gemeinsamen Architektur der neuronalen Aktivität abweichen? In diesem Artikel haben wir mathematische Methoden analog zu denen der Quantenmechanik und das Konzept des Phasenraums auf EEGs angewendet, die während der Ruhe und beim Ansehen von Filmen aufgezeichnet wurden, um räumliche und Übergangseigenschaften dynamischer neuronaler Aktivität zu extrahieren. Die Quantenmechanik wurde entwickelt, um die Dynamik der subatomaren Welt in Form von Wahrscheinlichkeitsamplituden und Zustandsdichten zu beschreiben. Quantensysteme (in der Schrödinger-Formulierung der Quantenmechanik) werden durch Wellenfunktionen beschrieben, die im Quadrat zu einer Wahrscheinlichkeitsverteilung stehen, was zum Verlust des lokalen Determinismus und der Heisenbergschen Unschärferelation führt (für einen Überblick/Einführung in das Thema siehe.

Diese Unschärferelation setzt dem Ort und dem Impuls eines Punktteilchens eine fundamentale Grenze.

Wenn die Position eines Teilchens bekannt ist, gibt es im Wesentlichen eine zugrunde liegende Unsicherheit in seinem Impuls (man kann nicht genau sagen, wie schnell es sich bewegt) und umgekehrt. Neben der Anpassung des Wellenfunktionsansatzes an die Quantenmechanik in dieser Arbeit haben wir auch ein Phasenraummodell verwendet. Der Phasenraum ist ein weit verbreitetes Werkzeug bei der Untersuchung dynamischer Systeme, bei dem die Positionsvariablen mit ihren konjugierten Impulsen gepaart werden, wodurch ein mehrdimensionaler Raum entsteht, der alle möglichen Konfigurationen des gegebenen Systems beschreibt. Dieser Raum umfasst den gesamten Bereich von Zuständen, in denen ein System existieren kann, jeder Punkt (in diesem Hyperraum) repräsentiert einen einzelnen Zustand des Systems. Der Phasenraum und seine verschiedenen Formalismen sind ein klassisches Konzept, und wir verwenden es einfach als ein weiteres Werkzeug zur Analyse der EEG-Daten. Hier werden die mathematischen Methoden der Quantenmechanik auf EEG-Daten angewendet, um einen Proxy für den Phasenraum zu extrahieren. Dieser Quasi-Quanten-Ansatz erzeugt natürlich die Konzepte „durchschnittlicher“ Ort, „durchschnittlicher“ Impuls und gipfelt in einer analogen Heisenberg-Unschärferelation.

In diesem Artikel postulieren wir, dass mit mathematischen Werkzeugen aus der Quantenmechanik ein zugrunde liegendes Muster realisiert werden kann, das repräsentativ für Aufgaben- und Ruhehirnaktivität ist, in dem Unterschiede zwischen den Bedingungen offensichtlich sind, aber in einem aufgabenunabhängigen konstanten Wert gipfeln. Es ist wichtig anzumerken, dass wir nicht behaupten, dass sich das Gehirn wie ein Quantenobjekt verhält, wie manche glauben. .

Vielmehr haben wir einige der analytischen Werkzeuge aus der Schrödinger-Formulierung der Quantenmechanik auf das Gehirn angewendet, um neue Einblicke in die Ruhe- und aufgabenbasierte Gehirndynamik zu gewinnen. Die Entwicklung dieses Modells untersucht nicht nur die Funktionen des Gehirns, sondern bietet auch einen neuartigen Ansatz zur Analyse der unzähligen Daten, die in den Neurowissenschaften verfügbar sind.

Ergebnisse

In diesem Artikel haben wir die Wahrscheinlichkeitsamplituden der Quantenmechanik angepasst, um neue Metriken für die Untersuchung von EEG-Daten zu definieren – die „durchschnittliche Position“ und „durchschnittliche Dynamik“ des EEG-Signals. Diese wurden aus unserer Definition von „Gehirnzuständen“ auf der Grundlage des Quasi-Quantenmodells konstruiert. Dadurch konnten wir die Häufigkeit ermitteln, mit der einzigartige Gehirnregionen von der Pseudowellenfunktion betreten werden, sowie den mittelwertbewerteten Phasenraum untersuchen. Schließlich wurde eine analoge Unsicherheitsbeziehung zu der der Quantenmechanik aufgestellt, wobei die vollständige mathematische Herleitung in den Methoden beschrieben ist.

Durchschnittliche Werte

Die „durchschnittliche Position“ der EEG-Daten wurde zuerst extrahiert, indem eine Hilbert-Transformation der vorverarbeiteten Zeitverläufe durchgeführt und dann eine Normalisierungsbeschränkung angewendet wurde. Typischerweise werden die Hilbert-transformierten Daten verwendet, um eine Metrik der Leistungsstreuung zu erzeugen oder um die Phase des Signals zu extrahieren. Stattdessen haben wir eine neue Normierungsbedingung eingeführt und damit eine Analogie zu den Wellenfunktionen der Quantenmechanik geschaffen. Wenn der Hilbert-transformierte Zeitverlauf der $j$-ten Elektrode als $\Psi _{j}$ bezeichnet wird, ist dies äquivalent zu

$\Psi _{j}(t)=A_{j}(t)\exp(i\theta _{j}(t))$

$(1)$

Mit $i={\sqrt {-1}}$. Wir haben dann die Normierungsbedingung auferlegt,

${\hat {\Psi }}_{j}(t)={\frac {\Psi _{j}(t)}{\sqrt {\sum _{j=1}^{92}|\Psi _{j}|^{2}}}}$

$(2)$

Die Summierung erstreckt sich auf 92, was den 92 Elektroden entspricht, die aus den ursprünglichen 129 auf der Kopfkappe ausgewählt wurden (Kanäle wurden für diese Analyse von Gesicht und Hals entfernt). Diese Normalisierungsbeschränkung ermöglichte es uns, die Wahrscheinlichkeit zum Zeitpunkt $t$ der $j$ j-ten Elektrode als zu definieren

$P_{j}(t)={\hat {\Psi }}_{j}^{*}(t)\times {\hat {\Psi }}_{j}(t)$

$(3)$

Wobei das * komplexe Konjugation bezeichnet. Wir können dann jeden Moment als einen „Gehirnzustand“ beschreiben, der (im Kontext dieses Modells) durch die „Wellenfunktion“ vollständig beschrieben wird. Dieser „Gehirnzustand“ spezifiziert das EEG-Signal und damit die interessierende Dynamik zu jedem Zeitpunkt eindeutig. Unter Verwendung dieser Definition von Wahrscheinlichkeit haben wir zwei interessierende Durchschnittsgrößen definiert. Die durchschnittliche Position und Impuls sind explizit gegeben durch,

$\langle x(t)\rangle =\sum _{j=1}^{92}x_{j}P_{j}(t)$ $\langle p_{x}(t)\rangle =m{d \over dt}\langle x(t)\rangle =m\sum _{j=1}^{92}x_{j}{d \over dt}P_{j}(t)$

$(4)$

Dasselbe gilt für $y$.

In der Praxis

Mit diesen beiden Gleichungen erzeugen wir unsere quasi-quantenmechanischen Analoga. Die zweite Gleichung ist eine Erweiterung des Satzes von Ehrenfest, der die durchschnittlichen Impulse eines Teilchens mit der zeitlichen Ableitung seiner durchschnittlichen Position in Beziehung setzt. Wobei wir einen Hamiltonoperator mit nur ortsabhängigem Potential angenommen haben. Beachten Sie, dass sich nur die Wahrscheinlichkeit mit der Zeit ändert, da die Positionen im Raum fixiert sind (Positionen der Elektroden). In dieser Arbeit wurde die Masse m sowohl für die $x$- als auch für die $y$-Impulse als Eins angenommen. Jede der 92 Elektroden wurde auf die horizontale Ebene projiziert, somit wurde die $j$-te Elektrode durch einen eindeutigen $(x_{j},y_{j})$-Punkt beschrieben.

Wir haben dieses Modell zuerst untersucht, indem wir die 92 Elektroden in acht Regionen auf der Kopfhaut gruppiert haben: Anterior L/R, Posterior L/R, Parietal L/R, Occipital L/R und die Wahrscheinlichkeiten jeder Elektrode in der Region wurden summiert, um a zu ergeben Wahrscheinlichkeit auf Regionsebene. Abbildung 1A zeigt die$(x_{j},y_{j})$ positionen jeder Elektrode, wobei verschiedene Farben jede der acht Gruppen darstellen. Abbildung 1B zeigt die Häufigkeit des Betretens jeder Region, gruppiert nach den vier Aufgabenbedingungen und zwei Ruhebedingungen. Dies spiegelt die normalisierte Anzahl regionaler Wahrscheinlichkeiten integriert über die Zeit wider. Wir fanden heraus, dass jede Frontzahnregion im Ruhezustand häufiger betreten wurde, als wenn die Probanden sich mit einem der beiden Filme beschäftigten. Insbesondere die vorderen linken und rechten Regionen hatten eine signifikante Veränderung innerhalb des Stimulus, mit $P<0.001$ (Tukey angepasst) für Taken Rest—Taken, Taken Rest—Taken Scrambled, BYD Rest—BYD und BYD Rest—BYD Scrambled. Dies steht im Einklang mit den Ergebnissen von Axelrod und Kollegen, die zeigten, dass eine Aktivierung in der Frontalregion mit Gedankenwanderungen verbunden war. Wir fanden eine Frequenzunterdrückung in den hinteren Regionen und eine Zunahme der vorderen Frequenz in Ruhe im Vergleich zu den stimulierten Bedingungen, was mit fMRT-Studien übereinstimmt, die eine erhöhte Aktivierung im hinteren cingulären Kortex und im medialen präfrontalen Kortex während der Ruhe zeigen. Dies deutet darauf hin, dass unser Modell die frontale Tendenz erfasst, die mit der Gehirnaktivität im Ruhezustand verbunden ist.

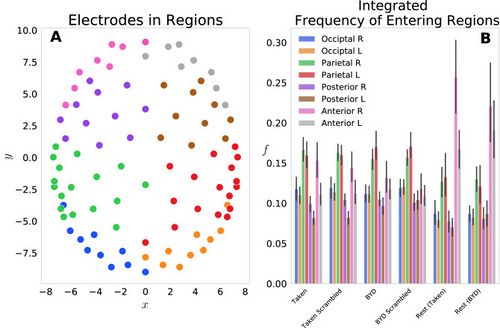
Abbildung 1: (A) Elektrodenpositionen für jede der 92 Elektroden auf der Kopfkappe von Electrical Geodesics Inc. Elektroden wurden auf eine horizontale Ebene mit der Nase in positiver y-Richtung projiziert. Die Elektroden wurden farbcodiert, um die Bestandteile der 8 Gruppen für die Frequenzanalyse anzuzeigen, nämlich okzipital links (blau)/rechts (orange), parietal links (grün)/rechts (rot), posterior links (lila)/ rechts (braun) und anterior links (rosa)/rechts (grau). (B) Histogramme, die die Häufigkeit des Betretens jeder Region fG darstellen, werden für die sechs getesteten Bedingungen angezeigt. Beim Vergleich der Ruhe vor dem Stimulus und der jeweiligen stimulierten Bedingung ist eine signifikante Änderung innerhalb des Stimulus zwischen jeder der vorderen linken und rechten Regionen vorhanden (P < 0,001, Tukey-korrigiert.). Fehlerbalken zeigen das 1-Standardabweichungs-Konfidenzintervall an.

Phasenraum

Wir haben auch den mittelwertigen Phasenraum dieses Systems untersucht. Der Phasenraum für jedes Subjekt wurde als durchschnittliche Position und Impuls entlang der aufgetragen $(\langle x(t)\rangle ,\langle p_{x}(t)\rangle )$Richtung$(\langle x(t)\rangle ,\langle p_{x}(t)\rangle )$oder als durchschnittliche Position und Impuls entlang der $x$ Richtung$(\langle y(t)\rangle ,\langle p_{y}(t)\rangle )$. Abbildung 2 zeigt die Schwerpunkte der Phasenraum-Streudiagramme für jedes Subjekt mit einer Ellipse, die das Konfidenzintervall einer Standardabweichung darstellt. Beachten Sie, dass Werte nur für die intakten Stimuli angegeben werden, da eine Varianzanalyse zeigt, dass die verschlüsselten und intakten Filme im Phasenraum nicht zu unterscheiden sind ($P<0.85$, Tukey angepasst). Abbildung 2A und B zeigen die Projektion des Phasenraumschwerpunktes auf die aufgespannte Ebene $x$ Und $p_{x}$ für „Pang! You’re Dead“ bzw. „Taken“ und Abb. 2C und D ($y,p_{y}$) Ebene. Die durchschnittliche Position entlang der $y$ Achse $(\langle y\rangle )$denn der intakte Stimulus („BYD“ und „Taken“) und ihre verschlüsselten Formen unterscheiden sich signifikant von den Gegenstücken mit Ruhe vor dem Stimulus $P<0.001$ (Tukey angepasst), während die aufgabenpositiven und ruhenden Schwerpunkte in der nicht unterscheidbar sind $x$ Ebene ($P<0.05$, Tukey angepasst). Die Mittelwerte der Gruppe sind in Tabelle 11 zusammen mit ihren Standardabweichungen angegeben. Diese Werte sind der gemittelte Wert der Schwerpunkte (Mittelwert der innerhalb der Stimulus-Mittelpunkte in Abb. 2) für die jeweilige Position/Impulse innerhalb jeder Stimulus-Ebene. Wie auch in Fig. 2C und D zu sehen ist, gibt es einen bemerkenswerten Unterschied von einer Größenordnung für$\langle y\rangle$zwischen den Ruhe- und Aufgabenbedingungen, jedoch keine deutlichen Unterschiede in $x$, $\langle p_{x}\rangle$ order $\langle p_{y}\rangle$

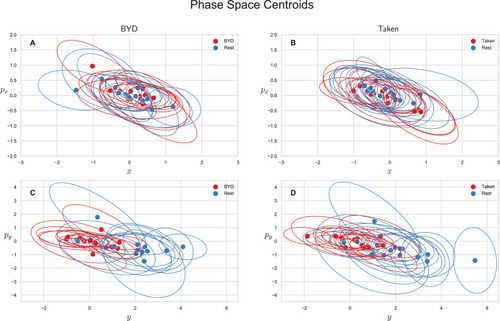
Abbildung 2: Mittlere Phasenraumschwerpunkte für jedes Subjekt. Ellipsen repräsentieren das 1-Standardabweichungs-Konfidenzintervall. Zentroide für die verschlüsselten Stimuli wurden weggelassen, da sie von intakten Stimuli nicht zu unterscheiden sind (P > 0,85) (A) Zentroide für „Bang! Du bist tot“ entlang der x-Richtung. (B) Schwerpunkte für „genommen“ entlang der x-Richtung. (C) Schwerpunkte für „Bang! Du bist tot“ entlang der y-Richtung. (D) Schwerpunkte für „genommen“ entlang der y-Richtung. Unterschiede sind nur in der y-Richtung erkennbar (P < 0,001, Tukey-korrigiert), was auf das höhere Maß an anteriorer Aktivierung hinweist, wie in Abb. 1 angegeben.

Tabelle 1

Gruppenmittelwerte der Schwerpunkte.

Stimulus	$\langle x\rangle$	$\langle y\rangle$	$\langle p_{x}\rangle$	$\langle p_{y}\rangle$
Vergriffen	$(-1.4\pm 5.8)\times 10^{-1}$	$(2.4\pm 8.0)\times 10^{-1}$	$(-5.8\pm 27.0)\times 10^{-2}$	$(-1.0\pm 4.1)\times 10^{-1}$
Rührei genommen	$(-7.7\pm 35.0)\times 10^{-2}$	$(1.1\pm 9.3)\times 10^{-1}$	$(4.1\pm 13.0)\times 10^{-2}$	$(6.3\pm 35.0)\times 10^{-2}$
Knall! Du bist tot	$(1.2\pm 4.7)\times 10^{-1}$	$(3.5\pm 74.0)\times 10^{-2}$	$(2.6\pm 33.0)\times 10^{-2}$	$(-3.0\pm 42.0)\times 10^{-1}$
Knall! Du bist tot verschlüsselt	$(1.4\pm 5.7)\times 10^{-1}$	$(-2.6\pm 7.5)\times 10^{-1}$	$(-1.5\pm 2.8)\times 10^{-1}$	$(-5.5\pm 53.0)\times 10^{-2}$
Ruhe (vorher genommen)	$(-1.3\pm 4.6.0)\times 10^{-1}$	$(2.0\pm 1.4)\times 10^{0}$	$(9.1\pm 19.0)\times 10^{-2}$	$(-6.3\pm 7.3)\times 10^{-1}$
Ruhe (vor BYD)	$(1.1\pm 66.0)\times 10^{-3}$	$(1.9\pm 1.2)\times 10^{0}$	$(1.0\pm 26.0)\times 10^{-2}$	$(-4.3\pm 7.5)\times 10^{-1}$

Signifikante Unterschiede werden nur für den Rest festgestellt, der vor Taken and Bang erworben wurde! Sie sind tot, wenn Sie die durchschnittliche y-Position mit einem ihrer Aufgabengegenstücke vergleichen (verschlüsselter und intakter Stimulus).

Gruppenmittelwerte der Schwerpunkte.

Diese Analyse ergab zwei bemerkenswerte Ergebnisse. Erstens fehlten signifikante Unterschiede in den Impulsen des Gehirns entlang der x- und y-Richtung. Zweitens unterschieden sich die Durchschnitte in Momenta auf Gruppenebene nicht signifikant von 0. Die positiven oder negativen Impulse kommen von der konkurrierenden zeitlichen Ableitung der Wahrscheinlichkeit und des Ortes der Elektrode. Da die Impulse durchschnittlich 0 betragen, gibt es eine gleiche Anzahl anteriorer und posteriorer Elektroden mit sowohl Zunahmen als auch Abnahmen in der Wahrscheinlichkeit.

Außerdem untersuchten wir Änderungen der Wahrscheinlichkeitswerte sowohl im Ruhezustand als auch im aktiven Zustand. Animationen der Wahrscheinlichkeitsverteilungen sind in Ergänzungsmaterial 1 enthalten. In diesen Animationen werden die Unterschiede in Ruhe und Aufgabe durch die zeitliche Entwicklung der Wahrscheinlichkeit deutlich.

Unschärferelation

Trotz der Bestätigung früherer neurowissenschaftlicher Ergebnisse und des offensichtlichen Erfolgs unseres Quasi-Quantenmodells bleibt unsere oben gestellte Forschungsfrage nur halb beantwortet. Unter Verwendung dieses Modells stellten wir Unterschiede in den Wahrscheinlichkeitsverteilungen und den Phasenraumschwerpunkten in Ruhe im Vergleich zur Aufgabe fest. Wir suchten aber dennoch einen Parameter aus dem Modell, der in Ruhe und Aufgabe gleich bleibt. Dazu haben wir eine analoge Heisenbergsche Unschärferelation der Form

$\bigtriangleup x(t)\bigtriangleup p_{x}(t)\geq K_{brain}$

$(5)$

Tabelle 2 zeigt die Werte dieser Konstante ($K_{brain}$) unter allen Bedingungen erfasst, sowie der Maximalwert, der Mittelwert und die Standardabweichung. Wir haben festgestellt, dass dieses Quasi-Quantenmodell zu einem konstanten Minimalwert über führt$\Delta x(t)\Delta p_{x}(t)$Und $\Delta y(t)\Delta p_{y}(t)$ von $0,78\pm 0,41{\tfrac {cm^{2}}{4ms}}$ mit $T=0,P=1$. Beachten Sie die Einheit von${\tfrac {cm^{2}}{4ms}}$ ist ein Ergebnis davon, dass das EEG bei 250 Hz abgetastet wird und die Masse als Einheit angenommen wird. Darüber hinaus bleiben der Durchschnittswert und die Standardabweichung dieser Größen über die Bedingungen hinweg konsistent mit einem Durchschnittswert von $9,3\pm 4,4{\tfrac {cm^{2}}{4ms}}$ ($T=0,P=1$) und einer Standardabweichung von $18\pm 29{\tfrac {cm^{2}}{4ms}}$( $T=0,P=1$). Bemerkenswerterweise variiert der Maximalwert zwischen den Bedingungen, wobei der größte Wert auftritt, während die Probanden den intakten Clip von Bang! Du bist tot. Obwohl die durchschnittliche Position des Signals entlang der y-Richtung in Ruhe anders ist als während einer Aufgabe ($P<0.001$) führt die quasi-quantenmathematische Methodik zu einem konstanten Unsicherheitswert. Bemerkenswerterweise zeigen die Werte in der Tabelle, dass die durchschnittliche Unsicherheit und die minimale Unsicherheit unter verschiedenen Bedingungen gleich sind, obwohl die Maxima um mehr als zwei Größenordnungen variieren. Dies verleiht der Idee, dass diese Unsicherheitsrelation die Ähnlichkeiten des Gehirns über die sehr unterschiedlichen Bedingungen hinweg erfasst, weitere Glaubwürdigkeit. Abbildung 3 zeigt die Wahrscheinlichkeitsverteilung zu dem Zeitpunkt, der dem Unsicherheitsminimum für $x$ und $y$ entspricht

Tabelle 2

Verschiedene Werte, die aus den Zeitverläufen der Produkte extrahiert wurden $\Delta x(t)\Delta p_{x}(t)$ and $\Delta y(t)\Delta p_{y}(t)$.

Stimulus	$\Delta x\Delta p_{x}$	$\Delta y\Delta p_{y}$	$\Delta x\Delta p_{x}$	$\Delta y\Delta p_{y}$	$\Delta x\Delta p_{x}$	$\Delta y\Delta p_{y}$	$\Delta x\Delta p_{x}$	$\Delta y\Delta p_{y}$
Vergriffen	${\textstyle (7\pm 2.1)10^{-1}}$	${\textstyle (7.2\pm 1.8)10^{-1}}$	${\textstyle (1.9\pm 1.0)10^{3}}$	${\textstyle (1.4\pm 0.8)10^{3}}$	${\textstyle (8.2\pm 2.2)10^{0}}$	${\textstyle (8.2\pm 2.2)10^{0}}$	${\textstyle (1.4\pm 0.4)10^{1}}$	${\textstyle (1.3\pm 0.4)10^{1}}$
Rührei genommen	${\textstyle (6.4\pm 2.6)10^{-1}}$	${\textstyle (6.8\pm 2.1)10^{-1}}$	${\textstyle (1.7\pm 1.2)10^{3}}$	${\textstyle (2.1\pm 2.2)10^{3}}$	${\textstyle (8.1\pm 1.9)10^{0}}$	${\textstyle (7.8\pm 2.0)10^{0}}$	${\textstyle (1.4\pm 0.4)10^{1}}$	${\textstyle (1.4\pm 0.7)10^{1}}$
Knall! Du bist tot	${\textstyle (7.6\pm 4.9)10^{-1}}$	${\textstyle (7.5\pm 3.1)10^{-1}}$	${\textstyle (0.1\pm 3.1)10^{5}}$	${\textstyle (0.7\pm 1.4)10^{4}}$	${\textstyle (9.4\pm 6.7)10^{0}}$	${\textstyle (8.3\pm 3.6)10^{0}}$	${\textstyle (4.1\pm 8.9)10^{1}}$	${\textstyle (2.7\pm 3.9)10^{1}}$
Knall! Du bist tot verschlüsselt	${\textstyle (7.4\pm 3.2)10^{-1}}$	${\textstyle (7.1\pm 2.9)10^{-1}}$	${\textstyle (2.5\pm 1.2)10^{3}}$	${\textstyle (2.5\pm 1.6)10^{3}}$	${\textstyle (9.3\pm 5.1)10^{0}}$	${\textstyle (8.6\pm 4.4)10^{0}}$	${\textstyle (1.6\pm 0.7)10^{1}}$	${\textstyle (1.5\pm 0.8)10^{1}}$
Ruhe (vorher genommen)	${\textstyle (9.7\pm 4.2)10^{-1}}$	${\textstyle (1.1\pm 0.6)10^{0}}$	${\textstyle (3.5\pm 3.1)10^{2}}$	${\textstyle (3.5\pm 1.7)10^{2}}$	${\textstyle (9.6\pm 2.1)10^{0}}$	${\textstyle (1.3\pm 0.4)10^{1}}$	${\textstyle (1.5\pm 0.8)10^{1}}$	${\textstyle (1.9\pm 0.7)10^{1}}$
Ruhe (vor BYD)	${\textstyle (6.3\pm 3.7)10^{-1}}$	${\textstyle (8.6\pm 6.1)10^{-1}}$	${\textstyle (3.7\pm 2.0)10^{2}}$	${\textstyle (4.3\pm 2.5)10^{2}}$	${\textstyle (8.7\pm 3.3)10^{0}}$	${\textstyle (1.2\pm 0.6)10^{1}}$	${\textstyle (1.4\pm 0.5)10^{1}}$	${\textstyle (1.9\pm 0.8)10^{1}}$

Betrachtet man den Mindestwert, den diese Produkte für jedes Fach erreichen, sehen wir einen konstanten Wert in x und y von$0,78\pm 0,41{\tfrac {cm^{2}}{4ms}}$, einen Durchschnittswert von $9,3\pm 4,4{\tfrac {cm^{2}}{4ms}}$ und eine konstante Standardabweichung von $18\pm 29{\tfrac {cm^{2}}{4ms}}$. Die Einheit von ${\tfrac {cm^{2}}{4ms}}$ ergibt sich aus der Abtastung von 250 Hz. Maximalwerte unterscheiden sich je nach Stimulation. Die Werte werden als Mittelwert über die Probanden plus oder minus 1 Standardabweichung angegeben.

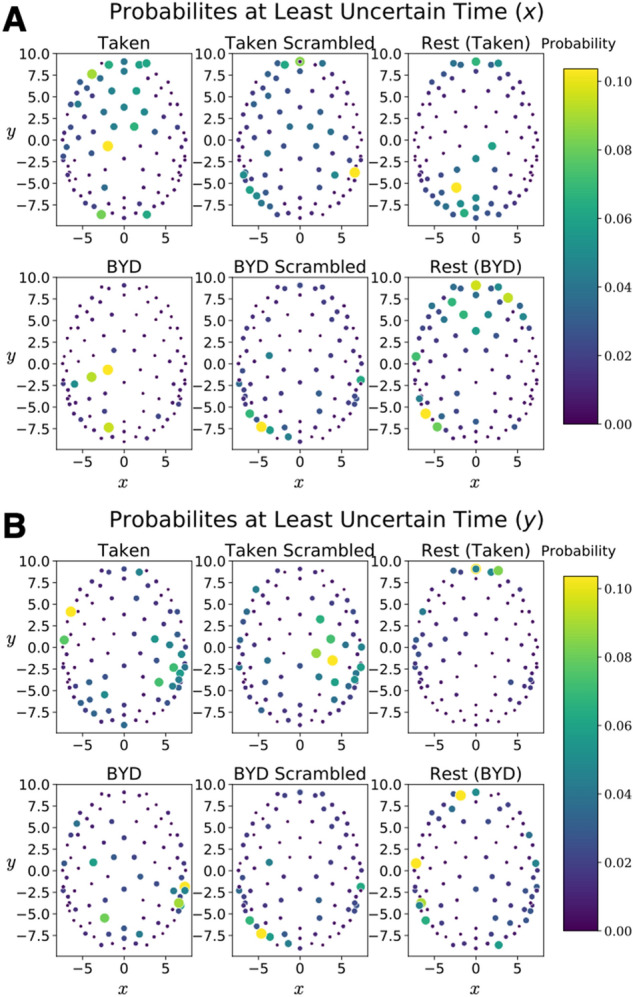
Abbildung 3: Wahrscheinlichkeitskarten, die dem am wenigsten unsicheren Zeitpunkt für jede der sechs experimentellen Bedingungen entsprechen. (A) Die Wahrscheinlichkeiten, die zu der minimalen Unsicherheit führen, definiert durch das Minimum von $\Delta x(t)\Delta p_{x}(t)$. (B) Die Wahrscheinlichkeiten, die zu der minimalen Unsicherheit führen, definiert durch das Minimum von $\Delta y(t)\Delta p_{y}(t)$. Ein Thema wird für alle Taken-Stimuli angezeigt und ein anderes für alle Bang! Du bist tot Reize.

Diskussion

In der aktuellen Studie untersuchten wir das räumliche Ausmaß und die damit verbundenen Übergangseigenschaften der neuronalen Aktivität im Gehirn unter aktiven und Ruhebedingungen und ob ähnliche zugrunde liegende Netzwerkeigenschaften existieren. Wir fanden heraus, dass die Anwendung der Hilbert-Transformation auf die EEG-Daten und deren Normalisierung (Gleichung 2) dem EEG-Signal über das Gehirn (Gleichung 3) eine probabilistische Struktur auferlegt, die wir verwendeten, um die Wahrscheinlichkeit von räumlichen Aktivitätsmustern zusammen mit Übergängen zu identifizieren in Aktivität über die Kopfhaut. Wir fanden mehr anteriore Aktivität während der Ruhe im Vergleich zum Anschauen von Filmen, sowohl im Amplituden- als auch im Phasenraum. Dieser Befund steht im Einklang mit früheren Ergebnissen, die eine erhöhte Aktivierung im vorderen Bereich während der Ruhe zeigten. Darüber hinaus konnten wir durch Normalisierung der Hilbert-transformierten EEG-Signale und Extrahieren von Durchschnittswerten, die denen der Wellenfunktionsformulierung der Quantenmechanik ähneln, die Unsicherheit in der „Position“ und dem „Impuls“ während der Ruhezeit und beim Ansehen von Filmen berechnen, die durch eingestellt werden die neue Konstante

$K_{brain}=0,78\pm 0,41{\tfrac {cm^{2}}{4ms}}$.

Es ist verlockend, die Konstante, die sich auf die „Position“ und den „Impuls“ der neuronalen Aktivität bezieht, mit einem fundamentalen Prinzip wie dem Heisenbergschen Unbestimmtheitsprinzip in Verbindung zu bringen. Was diese Ungewissheit bedeutet, ist jedoch noch unklar. Es könnte Grenzen für den Grad der Zugänglichkeit des Gehirns bedeuten; Zunehmende Informationen über den genauen Ort des Gehirnzustands (wie durch unsere Quasi-Quanten-„Wellenfunktionen“ beschrieben) werden eine größere Unsicherheit darüber erzeugen, wo er sich zu einem späteren Zeitpunkt befinden wird. Diese Ergebnisse bieten eine interessante Perspektive auf die Verbindung zwischen neuronaler Funktion und kognitiven Prozessen. Wenn zum Beispiel die „Wellenfunktion“ entlang eines Gedankengangs im Raum lokalisiert wird, werden wir abgelenkt, um die Unsicherheit zu erhöhen, was erklären könnte, warum Gedanken wandern und Gedanken flüchtig sind?

Ist der $K_{b}$ Wert, den wir über verschiedene Stimulusbedingungen konstant fanden, und unabhängig von der Anzahl der Elektroden, die zum Erfassen der Daten verwendet wurden? Um dies zu testen, haben wir die EEG-Elektroden von 92 auf 20 abgetastet und die gleiche Analyse wie im Haupttext durchgeführt. In Übereinstimmung mit 92 Kanälen fanden wir die anteriore Tendenz in Ruhe, aber wir stellten fest, dass die Verringerung der Elektroden auf 20 zu einer anderen Konstante führte $K_{b}=0,03\pm 0,02{\tfrac {cm^{2}}{4ms}}$ (Siehe Zusatzmaterial). Dies zeigt, dass das Modell in der Lage ist, die Unterschiede zwischen Ruhe und Aufgabe zu erfassen, aber möglicherweise muss eine montageabhängige Normalisierungsbedingung eingeführt werden.

Es ist wichtig zu beachten, dass Unsicherheitswerte dieser Form allen konjugierten Fourier-Variablen inhärent sind, da sich ein Wert in einer Variablen ausbreitet und in der anderen lokalisiert. Dies legt nahe, dass nach dem Definieren des Quadrats des zeitlichen Verlaufs der Hilbert-transformierten EEG-Elektrode als Wahrscheinlichkeit und dem Auferlegen der Eigenschaften eines Hilbert-Raums auf die Elektrodensignale ein Unsicherheitswert extrahiert werden kann. In der Quantenmechanik setzt diese Unsicherheit die Grenze für die nicht beobachtbaren Skalen. Dieser Ansatz wurde von der Notwendigkeit in der Neurowissenschaft nach neuartigen Modellen inspiriert, um bei der Interpretation von Neuroimaging-Daten zu helfen. Obwohl dies ein interessanter methodischer Fortschritt ist, müssen wir noch feststellen, ob die beobachtete Unsicherheit in den EEG-Daten durch ein neues Grundprinzip wie in der Quantenmechanik gestützt wird oder ob sie nur das Ergebnis der Bildung von zwei neuen konjugierten Fourier-Variablen aus der ist EEG-Signal.

Weitere Arbeiten müssen unternommen werden, um diese Konstante im Hinblick auf die reichhaltige Taxonomie von Aufgaben und Stimuli und unterschiedlichen Bewusstseinszuständen, die routinemäßig in der kognitiven Neurowissenschaft verwendet werden, zu erforschen. Diese Methodik könnte auf fMRI ausgedehnt werden, wo die BOLD-Zeitverläufe Hilbert-transformiert werden könnten, wodurch ein dreidimensionales Analogon des in diesem Artikel vorgestellten EEG-Modells entsteht.

Letztendlich stellte dieses Papier eine neuartige Methodik zur Analyse von EEG-Daten vor. Die Normalisierung der Daten und ihre Behandlung als Wahrscheinlichkeitsamplitude führte zu Parametern, die sich mit dem Vorhandensein oder Fehlen eines Stimulus änderten, während gleichzeitig ein konstanter Wert unabhängig vom Stimulus festgelegt wurde. Wir haben erfolgreich einen mathematischen Rahmen basierend auf den Formalismen der Quantenmechanik auf das Ruhe- und Aufgabenparadigma im EEG angewendet (ohne zu behaupten, dass das Gehirn ein Quantenobjekt ist). Da sich die Neurowissenschaften weiterentwickeln, müssen auch die ihr zur Verfügung stehenden Analysewerkzeuge entsprechend weiterentwickelt werden. Wir hoffen, dass dieses analytische Werkzeug zusammen mit den Fortschritten in der Modellierung und im maschinellen Lernen unser Verständnis der Natur des Bewusstseins unterstützen wird.

Methoden

Datenerfassung

28 gesunde Probanden wurden vom Brain and Mind Institute der University of Western Ontario, Kanada, rekrutiert, um an dieser Studie teilzunehmen. Vor dem Testen wurde von allen Teilnehmern eine schriftliche Zustimmung nach Aufklärung eingeholt. Die ethische Genehmigung für diese Studie wurde vom Health Sciences Research Ethics Board und dem Non-Medical Research Ethics Board der University of Western Ontario erteilt und die gesamte Forschung wurde in Übereinstimmung mit den relevanten Richtlinien/Vorschriften und in Übereinstimmung mit der Deklaration von Helsinki durchgeführt.

Als naturalistische Stimuli wurden in dieser Studie zwei spannende Filmclips verwendet. Ein Videoclip aus dem Stummfilm „Bang! Du bist tot“ und ein Audioausschnitt aus dem Film „Taken“ wurden 13 bzw. 15 Probanden sowohl in ihrer ursprünglichen intakten als auch verschlüsselten Form gezeigt. Vor den beiden Akquisitionen wurde ein Ruheabschnitt erworben, in dem die Probanden gebeten wurden, sich ohne offensichtliche Stimulation zu entspannen. Die Stimulus-Präsentation wurde mit dem Psychtoolbox-Plugin für MATLAB auf einem 15″ Apple MacBook Pro gesteuert. Audio wurde binaural mit einer angenehmen Hörlautstärke über Etymotics ER-1-Kopfhörer präsentiert.

EEG-Daten wurden unter Verwendung einer 129-Kanal-Kappe (Electrical Geodesics Inc. [EGI], Oregon, USA) gesammelt. Die Elektrodenimpedanzen wurden unter 50 kΩ gehalten, wobei die Signale bei 250 Hz abgetastet und auf den zentralen Scheitelpunkt (Cz) bezogen wurden. Unter Verwendung der EEGLAB MATLAB-Toolbox wurden verrauschte Kanäle identifiziert und entfernt und dann wieder in die Daten interpoliert. Ein Kolmogorov-Smirnov (KS)-Test an den Daten wurde verwendet, um Regionen zu identifizieren, die nicht gaußförmig waren. Eine unabhängige Komponentenanalyse (ICA) wurde dann verwendet, um Muster neuraler Aktivität, die für Augen- und Muskelbewegungen charakteristisch sind, visuell zu identifizieren, die anschließend aus den Daten entfernt wurden. Die EEG-Vorverarbeitung wurde individuell für jedes Subjekt und jeden Zustand durchgeführt.

Von den beiden getesteten Filmclips war der erste ein 8-minütiger Ausschnitt aus Alfred Hitchcocks TV-Stummfilm „Bang! Du bist tot". Diese Szene zeigt einen 5-jährigen Jungen, der den Revolver seines Onkels aufhebt. Der Junge lädt eine Kugel in die Waffe und spielt damit wie mit einem Spielzeug. Der Junge (und Betrachter) weiß selten, ob die Waffe eine Kugel in ihrer Kammer hat, und die Spannung baut sich auf, wenn der Junge die Kammer dreht, sie auf andere richtet und den Abzug drückt. Als Alternative zur visuellen Stimulation wurde auch ein 5-minütiger Audioausschnitt aus dem Film „Taken“ verwendet. Dieser Clip zeigt ein Telefongespräch, in dem ein Vater die Entführung seiner Töchter belauscht.

Außerdem wurden zwei „verwürfelte“ Kontrollreize verwendet – einer für jeden Film. Dies trennt die neuronalen Reaktionen, die durch die sensorischen Eigenschaften beim Ansehen oder Anhören der Filme ausgelöst werden, von denen, die an der Verfolgung der Handlung beteiligt sind. Die verschlüsselte Version von „Bang! Du bist tot“ wurde generiert, indem 1-Sekunden-Segmente isoliert und die Segmente pseudozufällig gemischt wurden, wodurch die zeitliche Kohärenz der Erzählung aufgehoben wurde. Die verschlüsselte Version von „Taken“ wurde durch spektrale Rotation des Tons erstellt, wodurch die Sprache nicht entzifferbar wurde. Die verschlüsselten Filmclips wurden vor den intakten Versionen präsentiert, um mögliche Übertragungseffekte der Erzählung zu vermeiden. Bevor die Versuchspersonen den verschlüsselten Stimulus beobachteten/hörten, wurde ein kurzes Segment des Ruhe-EEG erfasst.

Modell

Jede der j Elektroden wird durch ein geordnetes Paar beschrieben ($x_{j},y_{j},z_{j}$) im dreidimensionalen Raum. Um diese Analyse abzuschließen, wurden die Elektroden zunächst auf die ($x,y$) Ebene, wobei die Tiefe des Kopfes entfernt wird. Fig. 1A zeigt die Positionen jeder Elektrode in diesem 2D-Raum. Nach dieser Projektion wurden die Zeitverläufe für jede der 92 Elektroden Hilbert-transformiert und dann gemäß dem unter Verwendung von Gl. (2). In diesem Elektrodenpositionsraum wurde eine Wahrscheinlichkeit als Quadrat des Hilbert-transformierten Zeitverlaufs definiert (Gl. 3), analog zu den Wellenfunktionen der Quantenmechanik. Acht Regionen Anterior L/R, Posterior L/R, Parietal L/R, Occipital L/R) wurden dann durch Gruppieren der 92 Elektroden definiert, und die Eintrittshäufigkeiten in jede Region fG wurden durch Summieren der Wahrscheinlichkeitselektroden innerhalb der Gruppe erhalten. dann rechtzeitig integrieren.

$Prob_{G}(t)=\sum _{j=1}^{92}\Psi _{k}^{*}(t)\times \Psi _{k}(t);f_{G}={\tfrac {1}{T}}\sum _{j=1}^{T}Prob_{G}(t)$

$(6)$

wobei jede der acht mit dem Index bezeichneten Gruppen eine unterschiedliche Anzahl von konstituierenden Elektroden N hat. Hinter dem Hinterkopf links und rechts sind jeweils 10 Elektroden, im Scheitelbereich links und rechts sind jeweils 17 Elektroden, im Hinterkopf links und rechts dort sind 10 bzw. 11 Elektroden, und vorne links und rechts befinden sich 8 bzw. 9 Elektroden.

Nach Erhalt der Frequenzen auf Gruppenebene wurden Mittelwerte für Position und Impuls unter Verwendung von Gl. (4) und (5) (mit identischen Ausdrücken für y). Schließlich suchten wir zur Feststellung unserer analogen Unbestimmtheitsrelation Ausdrücke der Form

$\bigtriangleup x={\sqrt {\langle x^{2}(t)\rangle -\langle x(t)\rangle ^{2}}};\bigtriangleup p_{x}={\sqrt {\langle p_{x}^{2}(t)\rangle -\langle p_{x}(t)\rangle ^{2}}}$

$(7)$

Der Ausdruck for kann leicht auf die oben definierten Wahrscheinlichkeiten und Positionen angewendet werden, was zu dem ersten Term führt, der durch gegeben ist

$\langle x^{2}(t)\rangle =\sum _{j=1}^{92}P_{j}(t)x_{j}^{2}$

$(8)$

Und der zweite Term, der durch das Quadrat von Gl. (4). Die zweite Amtszeit von $\Delta P_{x}$ ist durch das Quadrat von Gl. (5), aber der erste Term ist nuancierter. Dies liegt an der komplexen Zahl, die zurückgegeben wird, wenn der Ableitungsoperator zweimal auf die Wahrscheinlichkeit angewendet wird. Um dies zu überwinden, wurden Fourier-Transformationen verwendet, um Gl. (5) in die Impulsbasis, die dann die effiziente Berechnung von ermöglichte $P_{x}^{2}(t)$.

Bezeichnung ${\tilde {P}}_{j}(t)$als Impuls-Raum-Wahrscheinlichkeit, erhalten durch eine zweidimensionale, nicht gleichförmige Fourier-Transformation der Ortsraum-Pseudowellenfunktion, Gl. (5) kann umgeschrieben werden als

$\langle p_{x}(t)\rangle =\sum _{j=1}^{92}{\tilde {P}}_{j}(t)p_{j}$

$(9)$

Führend zum ersten Term im zu schreibenden Ausdruck als,

$\langle p_{x}^{2}(t)\rangle =m^{2}\sum _{j=1}^{92}{\tfrac {x_{j}^{2}}{{\tilde {p}}_{j}(t)}}[{d \over dt}P_{j}(t)]^{2}$

$(10)$

Der FINUFFT-Python-Wrapper wurde verwendet, um die Fourier-Transformation unter Verwendung einer ungleichmäßigen 2d-FFT des Typs 3, 2d durchzuführen, und der zeitliche Minimalwert der Unsicherheitsrelation wurde gefunden. Punkte im Impulsraum wurden abgetastet $p_{x}\in [-4,4]$Und $p_{y}\in [-4,5]$ zusammen mit den zwei zusätzlichen Punkten ($[-5,-4]$) Und ($[-4,-5]$)

Abbildung 4 zeigt die Orts- und Impulswahrscheinlichkeiten jeweils in ihrer eigenen Basis. Eine Animation, die zeigt, wie sich diese im Laufe der Zeit für die verschiedenen Bedingungen entwickeln, ist in Ergänzungsmaterial 2 dargestellt.

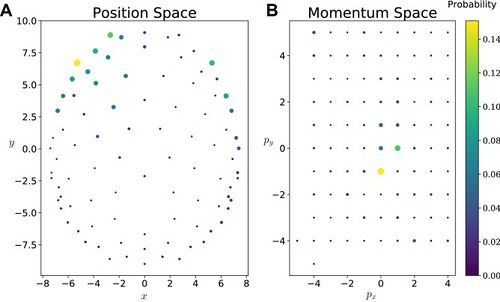
Abbildung 4: (A) Wahrscheinlichkeitsverteilung für ein einzelnes Subjekt in der Positionsbasis. (B) Momentum-Basis-Wahrscheinlichkeitsverteilung für ein einzelnes Subjekt. Die für die Fourier-Transformation verwendeten Impulswerte sind durch die Punktpositionen angegeben. Punkte sind farb-/größencodiert, um den Wahrscheinlichkeitswert an dieser Stelle darzustellen.

Um die in Tabelle 2 angegebenen Werte zu berechnen, wurde für jedes Subjekt der entsprechende Wert gefunden, und diese wurden verwendet, um den hier angegebenen Gruppendurchschnitt zu berechnen.

Ergänzende Angaben

Ergänzende Zahlen.(28M, docx)

Ergänzende Informationen.(375K, docx)

Danksagungen

Wir möchten Silvano Petrarca für seine fortwährende Unterstützung bei der Entwicklung des Modells danken. Diese Studie wurde vom NSERC Discovery Grant (05578–2014RGPIN), CERC (215063), CIHR Foundation Fund (167264) finanziert. AMO ist Fellow des CIFAR Brain, Mind and Consciousness Program.

Autorenbeiträge

N.J.M.P., C.M. und G. L. führten die Analyse durch. A. S., B. S. und N.J.M.P. das Modell entwickelt. ALS. und B.S. überwachte die Analyse. N.J.M.P., A.S., G.L. und B.S. schrieb das Manuskript. A.M.O. überarbeitete das Manuskript.

Konkurrierende Interessen

Die Autoren erklären keine konkurrierenden Interessen.

Fußnoten

Anmerkung des Herausgebers

Springer Nature bleibt neutral in Bezug auf Zuständigkeitsansprüche in veröffentlichten Karten und institutionellen Zugehörigkeiten.

Diese Autoren haben zu gleichen Teilen beigetragen: Bobby Stojanoski und Andrea Soddu.

Ergänzende Angaben

Die Online-Version enthält ergänzendes Material, das unter 10.1038/s41598-021-97960-7 verfügbar ist.

Artikelinformationen

Sci Rep. 2021; 11: 19771.

Published online 2021 Oct 5. doi: 10.1038/s41598-021-97960-7

PMCID: PMC8492705

PMID: 34611185

Nicholas J. M. Popiel,^1,2 Colin Metrow,¹ Geoffrey Laforge,³ Adrian M. Owen,^3,4,5 Bobby Stojanoski,^#4,6 and Andrea Soddu^#1,3

¹The Department of Physics and Astronomy, The University of Western Ontario, London, ON N6A 5B7 Canada

²Cavendish Laboratory, University of Cambridge, Cambridge, CB3 0HE UK

³The Brain and Mind Institute, The University of Western Ontario, London, ON N6A 5B7 Canada

⁴The Department of Psychology, The University of Western Ontario, London, ON N6A 5B7 Canada

⁵The Department of Physiology and Pharmacology, The University of Western Ontario, London, ON N6A 5B7 Canada

⁶Faculty of Social Science and Humanities, University of Ontario Institute of Technology, 2000 Simcoe Street North, Oshawa, ON L1H 7K4 Canada

Andrea Soddu, Email: asoddu@uwo.ca

Corresponding author.

1. Contributed equally.

Received 2021 Apr 28; Accepted 2021 Aug 30.

Copyright © The Author(s) 2021

Offener Zugang

Dieser Artikel ist unter einer Creative Commons Attribution 4.0 International License lizenziert, die die Verwendung, gemeinsame Nutzung, Anpassung, Verbreitung und Reproduktion in jedem Medium oder Format erlaubt, solange Sie den ursprünglichen Autor (die ursprünglichen Autoren) und die Quelle angemessen erwähnen, a Link zur Creative-Commons-Lizenz und geben Sie an, ob Änderungen vorgenommen wurden. Die Bilder oder andere Materialien von Drittanbietern in diesem Artikel sind in der Creative Commons-Lizenz des Artikels enthalten, sofern in einer Quellenangabe für das Material nichts anderes angegeben ist. Wenn Material nicht in der Creative-Commons-Lizenz des Artikels enthalten ist und Ihre beabsichtigte Nutzung durch gesetzliche Bestimmungen nicht gestattet ist oder die zulässige Nutzung überschreitet, müssen Sie die Genehmigung direkt vom Urheberrechtsinhaber einholen. Um eine Kopie dieser Lizenz anzuzeigen, besuchen

Sie http://creativecommons.org/licenses/by/4.0/.

Artikel aus wissenschaftlichen Berichten werden hier mit freundlicher Genehmigung von == Nature Publishing Group == zur Verfügung gestellt

Bibliography & references

Masticationpedia is a charity, a not-for-profit organization operating in dentistry medical research,
particularly focusing on the field of the neurophysiology of the masticatory system
 

Home

Introduction

Latest chapter

Ed. Lab

Donate

Contacts