Masticationpedia

La logica del linguaggio probabilistico

Page Discussion
Go to top
This page is a translated version of the page The logic of probabilistic language and the translation is 65% complete.
Other languages:

In questo capitolo, discuteremo la logica del linguaggio accoppiata con la probabilità matematica. Abbiamo visto che logica classica da sola non è sufficiente per determinare diagnosi accurate; quindi, viene fornita una panoramica concettuale e formale sul perché la probabilità può essere molto utile. Fornendo illustrazioni di casi clinici, vedremo come la logica del linguaggio probabilistico sia in grado di fornirci una diagnosi differenziale in modo “abbastanza buono”.

La conclusione è che è possibile dimostrare che, anche con l'aggiunta del solo ragionamento probabilistico, non è possibile determinare diagnosi esatte, quindi si cercano altri arricchimenti per il nostro linguaggio.

 

Masticationpedia

 

Logica probabilistica del linguaggio in medicina

Ogni idea scientifica (che sia in medicina, architettura, ingegneria, chimica o qualsiasi altra materia), quando viene messa in pratica, è soggetta a piccoli errori e incertezze. La matematica - attraverso la teoria della probabilità e l'inferenza statistica - aiuta a controllare con precisione e quindi a contenere queste incertezze. Va sempre considerato che in tutti i casi pratici gli esiti dipendono anche da molti altri fattori esterni alla teoria, siano essi condizioni iniziali e ambientali, errori sperimentali, o altro.

Tutte le incertezze su questi fattori rendono probabilistica la relazione teoria-osservazione. Nell'approccio medico, ci sono due tipi di incertezza che pesano di più sulle diagnosi: incertezza soggettiva e casualità.[1][2]

Diventa essenziale in questo scenario, quindi, distinguere tra queste due incertezze e mostrare che il concetto di probabilità ha significati diversi in questi due contesti.

Cercheremo di esporre questi concetti legando ogni passaggio cruciale all'approccio clinico che è stato riportato nei capitoli precedenti e in particolare l'approccio in ambito odontoiatrico e neurologico nel contendersi il primato della diagnosi per la nostra cara Mary Poppins.

Incertezza soggettiva e casualità

Immaginiamo di chiedere a Mary Poppins quale dei due colleghi medici – il dentista o il neurologo – ha ragione.

La domanda creerebbe una sorta di agitazione basata sull'incertezza interiore; quindi, le nozioni di certezza e incertezza si riferiscono a stati epistemici soggettivi degli esseri umani e non a stati del mondo esterno, perché in quel mondo non c'è certezza o incertezza. In questo senso, come abbiamo accennato, esistono un mondo interiore e un mondo fuori di noi che entrambi non rispondono a canoni di incertezza, ma di probabilità.

Mary Poppins può essere soggettivamente certa o incerta se soffra di TMD o di una forma neuropatica o neuromuscolare di OP: questo perché "incertezza" è uno stato soggettivo, epistemico, al di sotto della soglia della conoscenza e della credenza; da qui il termine.

Incertezza soggettiva

Senza ombra di dubbio il termine "soggettiva" spaventa molti, soprattutto coloro che intendono fare scienza inseguendo il sano ideale di "oggettività", così come questo termine è percepito dal senso comune. È quindi opportuno fare alcune precisazioni sull'uso di tale termine in questo contesto::

  • ‘Soggettivo’ indica che la valutazione della probabilità dipende dallo stato informativo dell'individuo che la esegue.
  • ‘Soggettivo’ non significa arbitraria..

La così detta "oggettività", come è percepita da chi è al di fuori della ricerca scientifica, viene definita quando una comunità di esseri razionali condivide lo stesso stato di informazione. Ma anche in questo caso, si dovrebbe parlare più propriamente di "intersoggettività" (ovvero la condivisione, da parte di un gruppo, di opinioni soggettive).

Nei casi clinici, proprio perché raramente i pazienti possiedono nozioni avanzate di medicina, bisogna considerare l'incertezza soggettiva. Convivere con l'incertezza vincola ad utilizzare un approccio probabilistico..

Casualità

La casualità indica la mancanza di connessione certa tra causa ed effetto. L'incertezza di una stretta unione fra la sorgente ed il fenomeno è tra i problemi più avversi nella determinazione di una diagnosi.

In un caso clinico un fenomeno Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A(x)} (come per esempio una malocclusione, crossbite, openbite, etc...) è associato casualmente ad un altro fenomeno Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B(x)} (come la degenerazione ossea della ATM); quando ci sono delle eccezioni per cui la proposizione logica Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A(x) \rightarrow B(x)} non è sempre vera (ma lo è il più delle volte). In tal caso si dirà che Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A(x) \rightarrow B(x)} non è sempre vera ma è probabile..

««Si passa da una condizione deterministica ad una stocastica.».»

Probabilità soggettiva e oggettiva

Si riprendono in questo capitolo alcuni argomenti già trattati sul fantastico libro di Kazem Sadegh-Zadeh[3], che affronta il problema della logica del linguaggio medico e ne rimoduliamo i contenti riferendoli al nostro caso clinico di Mary Poppins per una cmprensione più aderente ai contesti odontoiatrici..

Si dice che eventi casuali e soggettivamente incerti siano probabili e di conseguenza, la casualità e l'incertezza sono trattate come probabilità qualitative, comparative o quantitative.

Per chiarire meglio questo concetto torniamo all'esempio di Mary Poppins. Un medico, avendo sentito i suoi sintomi potrà dire che:

  1. Mary Poppins è probabilmente affetta da DTM ((termine qualitativo).).
  2. Mary Poppins è più probabile che sia affetta da DTM che da DOF neuropatico. (termine comparativo: numero dei casi diagnosticati di DTM rispetto a quelli DOF nOP..
  3. La probabilità che Mary Poppins sia affetta da DTM è dello 0,15 (termine quantitativo, rispetto alla popolazione).

Probabilità soggettiva

in un contesto di incertezza soggettiva umana, il dato probabilistico, qualitativo, comparativo e/o quantitativo, può essere interpretato come una misura dell'incertezza soggettiva da parte del clinico in modo da rendere numericamente rappresentabili gli "stati di convinzione"..

Ad esempio, dire che "la probabilità che Mary Poppins sia affetta da DTM è dello 0,15 dei casi è la stessa cosa che dire "nella misura del 15%, io credo che Mary Poppins sia affetta da DTM" il che significa che il grado di convinzione è il grado di probabilità soggettiva.

Probabilità oggettiva

D'altra parte, eventi e processi casuali non possono essere descritti da processi deterministici come "se A allora B". La statistica viene utilizzata per quantificare la frequenza di associazione tra A e B e per rappresentare le relazioni indeterministiche tra loro come un grado di probabilità che introduce il grado di probabilità oggettiva.

Sulla scia della crescente probabilizzazione dell'incertezza e della casualità in medicina dal diciottesimo secolo, il termine "probabilità" è diventato un elemento rispettato del linguaggio medico, della metodologia e dell'epistemologia.

Sfortunatamente i due tipi di probabilità, il soggettivo e l'oggettivo, non sono accuratamente differenziati in medicina ed in altre discipline. Rimane il fatto fondamentale che il significato più importante che la teoria della probabilità ha generato nella medicina, in particolare nei concetti di probabilità in eziologia, epidemiologia, diagnostica e terapia, sia il suo contributo alla nostra comprensione e rappresentazione della casualità medica.

Analisi probabilistico-causale

Da queste premesse si evince che la diagnosi clinica venga fatta mediante il cosiddetto metodo ipotetico-deduttivo indicato come D-N[4] (deductive-nomological model[5]). ma ciò non è realistico perché le conoscenze mediche utilizzate nel processo decisionale clinico contengono a malapena leggi deterministiche causali per consentire spiegazioni causali e quindi, formulare diagnosi cliniche tra l'altro nel contesto specialistico.Proviamo ad analizzare di nuovo il caso della nostra Mary Poppins provando questa volta un approccio probabilistico-causale.

Consideriamo un numero Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} di individui dove sono incluse persone che riferiscono Dolore Orofacciale che generalmente hanno una degenerazione ossea dell'Articolazione Temporomandibolare. Potrebbero, però, esserci anche altre cause apparentemente scollegate. Dobbiamo tradurre matematicamente la "rilevanza" che queste incertezze causali hanno nella determinazione di una diagnosi.

La rilevanza causale

Per fare ciò consideriamo il grado di rilevanza causale Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (cr)} di un evento Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_1} rispetto ad un evento Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_2} dove:

  • Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_1} = pazienti con degenerazione ossee dell'Articolazione Temporomandibolare.
  • Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_2} = pazienti che riferiscono Dolore Orofacciale.
  • Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_3} = pazienti senza degenerazione ossea dell'articolazione Temporomandibolare.

Utilizzeremo la probabilità condizionata Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(A \mid B)} , ovvero la probabilità che l'evento Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} si verifichi solo dopo che si è già verificato l'evento Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B} ..

Con queste premesse la rilevanza causale del campione Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle cr} di pazienti Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} è:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle cr=P(E_2 \mid E_1)- P(E_2 \mid E_3)}

dove

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(E_2 \mid E_1)} indica la probabilità che alcune persona (fra le Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} persone in considerazione)soffrono di Dolore Orofacciale causato da degenerazione dell'Articolazione Temporomandibolare,

mentre

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(E_2 \mid E_3)} indica la probabilità che altre persone (sempre tra gli Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} presi in considerazione) soffrano di Dolore Orofacciale condizionato da qualcosa differente dalla degenerazione ossea dell'Articolazione Temporomandibolare..

Poiché ogni probabilità Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(A \mid B)} è un valore compreso fra 

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0 }
 and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1 }
, il parametro Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (cr)}
  sarà un numero che è compreso fra  Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -1 }
 e  Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1 }
.

I significati che possiamo dare a questo numero sono i seguenti:

  • abbiamo i casi estremi (che nella realtà non si verificano mai) che sono:
  • Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle cr=1} che indica che l'unica causa del dolore orofacciale è la degenerazione ossea dell'ATM,,
  • Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle cr=-1} che indica che la causa del dolore orofacciale non è mai la degenerazione ossea dell'ATM ma è altro,,
  • Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle cr=0}  che indica che la probabilità che il dolore orofacciale sia causato da degenerazione ossea dell' ATM o da altro è esattamente identica,,
  • e i casi intermedi (che sono quelli realistici)
  • Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle cr>0} che indica che è più probabile che la causa del dolore orofacciale sia la degenerazione ossea dell'ATM,,
  • Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle cr<0} che indica che è più probabile che la causa del dolore orofacciale non sia la degenerazione ossea dell'ATM..


Secondo approccio clinico

(passa il mouse sulle immagini)

  • Figura 1: Paziente che riporta 'Dolore orofaccialenell'emilato destro'

  • Figura 2: Stratigrafia dell'ATM del paziente che mostra segni di appiattimento consolare ed osteofita

  • Figura 3: Tomografia Computerizzata della ATM

  • Figura 4: Assiografia consolare del paziente che mostra un appiattimento dei pattern masticatori del condilo destro

  • Figura. 5: Pattern Interferenziale EMG. La sovrapposizione delle tracce superiori corrispondono al massetere destro, le inferiori al massetere sinistro dei masseteri.


Sia allora Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(D)} la probabilità di trovare, nel campione delle nostre Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} persone, individui che presentano gli elementi appartenenti al suddetto set Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D=\{\delta_1,\delta_2,...,\delta_n\}}

Per poter usufruire delle informazioni fornite da questo set di dati s'introduce il concetto di partizione della rilevanza causale::

La partizione della rilevanza casuale

Sia sempre Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} il numero delle persone che abbiamo per condurre le analisi, se si divide (in base a determinate condizioni spiegate nel seguito) questo gruppo in Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} sottoinsiemi Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_i} con Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i=1,2,\dots,k} , si crea quello che viene definito un set di partizione Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pi} :
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pi = \{C_1, C_2,\dots,C_k \} \qquad \qquad \text{with} \qquad \qquad C_i \subset n , }

dove con il simbolismo Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_i \subset n } si indica che la sottoclasse Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_i} è contenuta in Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_i} è contenuta in Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} .

La partizione Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pi} , affinché possa essere definita di partizione della rilevanza causale deve possedere tali proprietà::

Per ogni sottoclasseFailed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_i} deve valere la condizione Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle rc=P(D \mid C_i)- P(D )\neq 0, } ovvero la probabilità di trovare nel sottogruppo Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_i}

una persona che abbia i sintomi e gli elementi appartenenti al set Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D=\{\delta_1,\delta_2,...,\delta_n\}} . non può essere identica a quella che si avrebbe nel trovarla "pescando" in tutto il campione Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} Una partizione causalmente rilevante di questo tipo si dice 'omogenea'..

  1. Ogni sottoinsieme Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_i} deve essere "elementare", cioè non deve essere ulteriormente diviso in altri sottoinsiemi, perché se questi esistessero non avrebbero alcuna rilevanza causale.

Ora supponiamo, per esempio, che il campione di popolazione Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} , a cui appartiene la nostra buona paziente Mary Poppins, sia una categoria di soggetti dai 20 ai 70 anni. Supponiamo anche che in questa popolazione abbiamo coloro che presentano gli elementi appartenenti all'insieme di dati Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D=\{\delta_1,.....\delta_n\}} che corrispondono ai test di laboratorio menzionati sopra e presentata in 'La logica del linguaggio classico'.

Let us suppose that in a sample of 10,000 subjects from 20 to 70 we will have an incidence of 30 subjects Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p(D)=0.003} showing clinical signs Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta_1} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta_4 }

. We preferred to use these reports for the demonstration of the probabilistic process because in the literature the data regarding clinical signs and symptoms for Temporomandibular Disorders have too wide a variation as well as too high an incidence in our opinion.[6][7][8][9][10][11]


An example of a partition with presumed probability in which TMJ degeneration (Deg.TMJ) occurs in conjunction with Temporomandibular Disorders (TMDs) would be the following:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(D| Deg.TMJ \cap TMDs)=0.95 \qquad \qquad \; } dove Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \C_1 \equiv Deg.TMJ \cap TMDs}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(D| Deg.TMJ \cap noTMDs)=0.3 \qquad \qquad \quad } dove Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_2\equiv Deg.TMJ \cap noTMDs}
dove Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_3\equiv no Deg.TMJ \cap TMDs}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(D| noDeg.TMJ \cap noTMDs)=0.001 \qquad \qquad \;} dove Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_4\equiv noDeg.TMJ \cap noTMDs}
«»


Clinical situations

These conditional probabilities demonstrate that each of the partition's four subclasses is causally relevant to patient data Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D=\{\delta_1,.....\delta_n\}} in the population sample Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle PO} . Given the aforementioned partition of the reference class, we have the following clinical situations:

  • Mary Poppins Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \in} degeneration of the temporomandibular joint Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cap} Temporomandibular Disorders
  • Mary Poppins Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \in} degeneration of the temporomandibular joint Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cap} no Temporomandibular Disorders
  • Mary Poppins Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \in} no degeneration of the temporomandibular joint Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cap} Temporomandibular Disorders
  • Mary Poppins Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \in} no degeneration of the temporomandibular joint Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cap} no Temporomandibular Disorders

To arrive at the final diagnosis above, we conducted a probabilistic-causal analysis of Mary Poppins' health status whose initial data were Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D=\{\delta_1,.....\delta_n\}} .

In general, we can refer to a logical process in which we examine the following elements:

  • an individual: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a}
  • its initial data set Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D=\{\delta_1,.....\delta_n\}}
  • a population sample Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} to which it belongs,
  • a base probability Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(D)=0,003}

At this point we should introduce too specialized arguments that would take the reader off the topic but that have an high epistemic importance for which we will try to extract the most described logical thread of the Analysandum/Analysans concept.

The probabilistic-causal analysis of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D=\{\delta_1,.....\delta_n\}} is then a couple of the following logical forms (Analysandum / Analysans[12]):

  • Analysandum Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \{P(D),a\}} : is a logical form that contains two parameters: probability Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(D)} to select a person who has the symptoms and elements belonging to the set Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D=\{\delta_1,\delta_2,...,\delta_n\}} , and the generic individual Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a} who is prone to those symptoms.
  • Analysan Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \{\pi,a,KB\}} : is a logical form that contains three parameters: the partition Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pi} , the generic individual Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a} belonging to the population sample Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle KB}  (Knowledge Base) which includes a set of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n>1}  statements of conditioned probability.

For example, it can be concluded that the definitive diagnosis is the following:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(D| Deg.TMJ \cap TMDs)=0.95} - this means that our Mary Poppins is 95% affected by TMDs, since she has a degeneration of the Temporomandibular Joint in addition to the positive data Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D=\{\delta_1,.....\delta_n\}}

Final considerations

We took a long and tortuous path to better understand the complexity encountered by the colleague struggling with the very heavy ethical responsibility of making a diagnosis. However, this task becomes even more complex when we need to be detailed and careful in making a differential diagnosis.

Here, we enter a delicate topic, that is connected with the epistemological contents and that first of all was reported in the "Introduction". We are talking about:

  • Interdisciplinarità:
    In science policy, it is generally recognized that science-based problem solving requires interdisciplinary research (IDR), as proposed by the EU project called Horizon 2020[13]. In a recent study, the authors focus on the question why researchers have cognitive and epistemic difficulties in conducting IDR. It is believed that the loss of philosophical interest in the epistemology of interdisciplinary research is caused by a philosophical paradigm of science called "Physics Paradigm of Science", which prevents recognition of important IDR changes in both the philosophy of science and research.
    The proposed alternative philosophical paradigm, called 'Engineering Paradigm of Science', makes alternative philosophical assumptions about aspects such as the purpose of science, the character of knowledge, the epistemic and pragmatic criteria for the acceptance of knowledge and the role of technological tools. Consequently, scientific researchers need so-called metacognitive scaffolds to assist them in the analysis and reconstruction of how 'knowledge' is constructed in different disciplines.
    In interdisciplinary research, metacognitive scaffolds help interdisciplinary communication analyse and articulate how the discipline builds knowledge[14][15]

This concept is linked to the previously discussed topic in which the colleague should be aware of his own 'Subjective Uncertainty' (due to a classic logic language 'sick or healthy') and of 'Objective Uncertainty' (due to a probabilistic logic language 'probably sick or probably healthy'). It is not complicated to prove this assertion: the uncertainty we are talking about derives from the fact that the elements, assertions, data, classes and subclasses mentioned and that build the apparatus of the logic of probabilistic's language: Analysandum Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \{P(D),a\}} e Analysan Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \{P(D),a\}} are elements that exist in a specific world, and in this case in a dental context in which the element Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle KB} of the process indisputably indicates a "basic knowledge" only in a specific dental context.

This conclusion confirmed by the dentist was the following:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(D| Deg.TMJ \cap TMDs)=0.95}

o meglio: it is my 95% belief that Mary Poppins is affected by TMDs since she has a degeneration of the temporomandibular joint in addition to the positivity of the data Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D=\{\delta_1,\dots\delta_n\}}

But something strange happens because out of nowhere, a researcher, who uses 'metacognitive scaffolds'[16] for an implementation in the analysis and reconstruction of how 'knowledge' is built in different disciplines, demands an answer to the following question from the dentist:

 
Question 2.jpg
    
«»


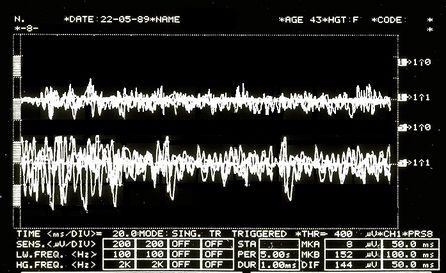
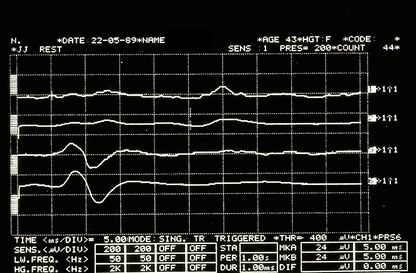
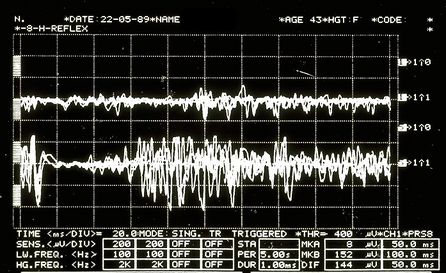
and increase the dose: submit Mary Poppins to the following trigeminal electrophysiological tests, label them as we did previously for the set data Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D=\{\delta_1,\dots\delta_n\}} generating another set containing a number Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m} of unknown data (not belonging to the purely dental branch) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C=\{\gamma_1,\dots\gamma_m\}} thereby creating an entirely new set that we will call Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{unknow}= D+C=\{\delta_1,\dots,\delta_n,\gamma_1,\dots,\gamma_m\}} (called Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{unknown}} precisely due to the presence of data unknown to the dental context).

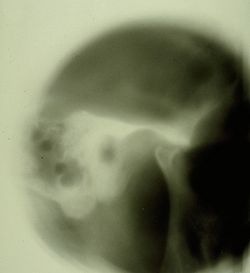
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta_1=}  Positive radiological report of the TMJ in Figure 2

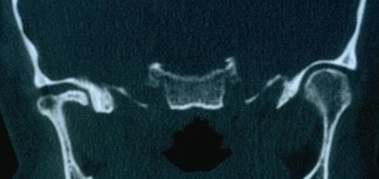
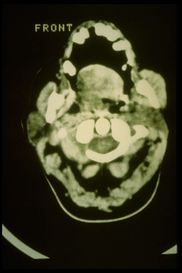
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta_2=} Positive CT report of the TMJ in Figure 3

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta_3=} Positive axiographic report of the condylar traces in Figure 4

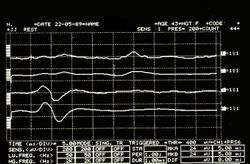
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta_4=} Asymmetric EMG interference pattern in Figure 5

Jaw jerk in Figure 6

Mechanical Silent Period in Figure 7

CT right masseter muscle in Figure 8


Third Clinical Approach

(hover over the images)


  • Figura 1: Patient reporting "Orofacial pain in the right hemilateral)

  • Figura 2: Patient's TMJ Stratigraphy showing signs of condylar flattening and osteophyte

  • Figura 3: Computed Tomography of the TMJ

  • Figura 4: Axiography of the patient showing a flattening of the chewing pattern on the right condyle

  • Figura 5: EMG Interferential Pattern. Overlapping upper traces corresponding to the right masseter, lower to the left masseter.

  • Figura 6: Jaw jerk electrophysiologically detected on the right (upper traces) and left (lower traces) masseters

  • Figura 7: Mechanical silent period detected electrophysiologically on the right (upper overlapping traces) and left (lower overlapping traces) masseters

  • Figura 8: Axial CT of the facial massif in which there is a marked hypertrophy of the right masseter


In this way it has been shown that, inevitably,

«{{{1}}}»


By exploring this perimeter line of the specialist context, we will create an area close to it which we will call the 'fuzzy zone' or 'fuzzy logic' which we will discuss in the next chapter.


 
Question 2.jpg
    
«in fact, for this reason we should also consider Fuzzy Logic Language»


 

 
[[{{{2}}}|{{{2}}}]]
Bibliography & references
  1. ↑ Vázquez-Delgado E, Cascos-Romero J, Gay-Escoda C, «Myofascial pain associated to trigger points: a literature review. Part 2: differential diagnosis and treatment», in Med Oral Patol Oral Cir Bucal, 2007».
    PMID:20173729
    DOI:10.4317/medoral.15.e639 
  2. ↑ Thoppay J, Desai B, «Oral burning: local and systemic connection for a patient-centric approach», in EPMA J, 2019».
    PMID:30984309 - PMCID:PMC6459460
    DOI:10.1007/s13167-018-0157-3 
  3. ↑ Sadegh-Zadeh Kazem, «Handbook of Analytic Philosophy of Medicine», Springer, 2012, Dordrecht».
    ISBN: 978-94-007-2259-0
    DOI:10.1007/978-94-007-2260-6     .
  4. ↑ Sarkar S, «Nagel on Reduction», in Stud Hist Philos Sci, 2015».
    PMID:26386529
    DOI:10.1016/j.shpsa.2015.05.006 
  5. ↑ (modello nomologico-deduttivo),, conosciuto come modello di Hempel, Hempel–Oppenheim model, Popper–Hempel model, o covering law model
  6. ↑ Pantoja LLQ, De Toledo IP, Pupo YM, Porporatti AL, De Luca Canto G, Zwir LF, Guerra ENS, «Prevalence of degenerative joint disease of the temporomandibular joint: a systematic review», in Clin Oral Investig, 2019».
    PMID:30311063
    DOI:10.1007/s00784-018-2664-y 
  7. ↑ De Toledo IP, Stefani FM, Porporatti AL, Mezzomo LA, Peres MA, Flores-Mir C, De Luca Canto G, «Prevalence of otologic signs and symptoms in adult patients with temporomandibular disorders: a systematic review and meta-analysis», in Clin Oral Investig, 2017».
    PMID:27511214
    DOI:10.1007/s00784-016-1926-9 
  8. ↑ Bonotto D, Penteado CA, Namba EL, Cunali PA, Rached RN, Azevedo-Alanis LR, «Prevalence of temporomandibular disorders in rugby players», in Gen Dent».
    PMID:31355769 
  9. ↑ da Silva CG, Pachêco-Pereira C, Porporatti AL, Savi MG, Peres MA, Flores-Mir C, De Luca Canto G, «Prevalence of clinical signs of intra-articular temporomandibular disorders in children and adolescents: A systematic review and meta-analysis», in Am Dent Assoc, 2016». - PMCID:26552334
    DOI:10.1016/j.adaj.2015.07.017 
  10. ↑ Gauer RL, Semidey MJ, «Diagnosis and treatment of temporomandibular disorders», in Am Fam Physician, 2015».
    PMID:25822556 
  11. ↑ Kohlmann T, «Epidemiology of orofacial pain», in Schmerz, 2002».
    PMID:12235497
    DOI:10.1007/s004820200000 
  12. ↑ Westmeyer H, «The diagnostic process as a statistical-causal analysis», in APA, 1975».
    DOI:10.1007/BF00139821
    Open Access logo green alt2.svg
    		 This is an Open Access resource!
     
  13. ↑ European Union, Horizon 2020
  14. ↑ Boon M, Van Baalen S, «Epistemology for interdisciplinary research - shifting philosophical paradigms of science», in Eur J Philos Sci, 2019».
    DOI:10.1007/s13194-018-0242-4      9(1):16.
  15. ↑ Boon M, «An engineering paradigm in the biomedical sciences: Knowledge as epistemic tool», in Prog Biophys Mol Biol, 2017».
    DOI:10.1016/j.pbiomolbio.2017.04.001 
  16. ↑ Boon M, Van Baalen S, «Epistemology for interdisciplinary research - shifting philosophical paradigms of science», in Eur J Philos Sci, 2019».
    PMID:30873248 - PMCID:PMC6383598
    DOI:10.1007/s13194-018-0242-4
    Open Access logo green alt2.svg
    		 This is an Open Access resource!
     
Wiki.png
Masticationpedia is a charity, a not-for-profit organization operating in dentistry medical research,
particularly focusing on the field of the neurophysiology of the masticatory system
 

 
Retrieved from "https://www.masticationpedia.org/index.php?title=The_logic_of_probabilistic_language/it&oldid=8090"