Logique du langage fuzzy
Dans ce chapitre, nous allons aborder la logique floue. Elle est dite floue car elle se caractérise par la gradualité : on peut attribuer à un objet une qualité qui peut avoir différents degrés de vérité.
Dans la première partie de ce chapitre, nous discuterons de la signification de la vérité graduelle sur le plan conceptuel, tandis que dans la deuxième partie, nous nous plongerons dans le formalisme mathématique en introduisant la fonction d'appartenance est l'élément qui nous permet de synthétiser mathématiquement les nuances de cette logique du langage. On a pu montrer qu'avec le raisonnement flou, contrairement aux logiques de langage précédentes, les diagnostics présentent moins d'incertitude. Malgré cela, on ressent toujours le besoin d'affiner la méthode linguistique et de l'enrichir de nouvelles "logiques".
Introduction
Nous en sommes arrivés là car, en tant que collègues, nous sommes très souvent confrontés à des responsabilités et à des décisions très difficiles à prendre et des questions telles que la conscience, l'intelligence et l'humilité entrent en jeu. Dans une telle situation, cependant, nous sommes confrontés à deux obstacles tout aussi difficiles à gérer celui d'un (base de connaissances), comme nous l'avons discuté dans le chapitre ‘Logic of probabilistic language’, limité dans le temps que nous codifions en et un limité dans le contexte spécifique (). Ces deux paramètres de l'épistémologie caractérisent l'âge scientifique dans lequel nous vivons. Aussi, tant le que le sont des variables dépendantes de notre phylogénie, et, en particulier, de notre plasticité conceptuelle et de notre attitude au changement.[1]
(Je vais vous donner un exemple pratique)
Combien de recherches ont été produites sur le sujet 'Logique floue' ?
Pubmed répond avec 2862 articles au cours des 10 dernières années,[2][3] ce qui nous permet de dire que le nôtre est actuel et suffisamment mis à jour. Cependant, si nous voulions attirer l'attention sur un sujet spécifique comme les «troubles temporo-mandibulaires», la base de données répondra avec jusqu'à 2 235 articles.[4] Par conséquent, si nous voulions vérifier un autre sujet comme "Douleur bucco-faciale", Pubmed nous donne 1 986 articles.[5] Cela signifie que le pour ces trois sujets au cours des 10 dernières années, il a été suffisamment mis à jour.
Si, maintenant, nous voulions vérifier l'interconnexion entre les sujets, nous remarquerons que dans les contextes sera le suivant :
- 'Troubles temporo-mandibulaires ET douleur orofaciale' 9 articles au cours des 10 dernières années[6]
- 'Troubles temporo-mandibulaires ET Douleurs bucco-faciales ET Logique floue' 0 articles des 10 dernières années[7]
L'exemple signifie que le est relativement à jour individuellement pour les trois sujets alors qu'il diminue considérablement lorsque les sujets entre les contextes sont fusionnés et plus précisément à 9 articles pour le point 1 et même à 0 articles pour le point 2. Ainsi, le est une variable dépendante du temps tandis que le est une variable cognitive dépendante de notre aptitude au progrès de la science, comme déjà mentionné – entre autres – dans le chapitre « Introduction ».
(Attend et regarde)
Nous avons terminé le chapitre précédent en affirmant que la logique d'un langage classique puis la logique probabiliste nous ont beaucoup aidés dans les progrès de la science médicale et du diagnostic mais portent implicitement en elles les limites de leur propre logique du langage, ce qui limite la vision de l'univers biologique. Nous avons également vérifié qu'avec la logique d'une langue classique - pour ainsi dire aristotélicienne - la syntaxe logique qui en est dérivée dans les diagnostics de notre Mary Poppins limite, en fait, la conclusion clinique.
(voir chapitre Classical Language's Logic),
soutient que : "tout patient normal qui est positif à l'examen radiographique de l'ATM a des TMD , en conséquence directe Mary Poppins étant positive (et étant également une patiente "normale") sur la radiographie des ATM alors Mary Poppins est également affectée par les TMD
La limitation du chemin logique qui a été suivi nous a conduit à entreprendre un chemin alternatif, dans lequel la nature bivalente ou binaire de la logique du langage classique est évitée et un modèle probabiliste est suivi. Le collègue dentiste, en effet, a changé le vocabulaire et a préféré une conclusion comme :
et qui est, que notre Mary Poppins est touchée à 95% par les TMD puisqu'elle a une dégénérescence de l'articulation temporo-mandibulaire soutenue par la positivité des données dans un échantillon de population . Cependant, nous avons également constaté que dans le processus de construction de la logique probabiliste (Analysandum qui nous a permis de formuler les conclusions diagnostiques différentielles susmentionnées et de choisir la plus plausible, il y a un élément crucial dans l'ensemble Analysand représenté par le terme qui indique, précisément, une « Base de connaissances » du contexte sur laquelle se construit la logique du langage probabiliste.
Nous avons donc conclu que le collègue dentiste aurait peut-être dû prendre conscience de sa propre « incertitude subjective » (affectée par les TMD ou nOP ?) et de son « incertitude objective » (probablement plus affectée par les TMDs ou nOP ?).
Pourquoi en sommes-nous arrivés à ces conclusions critiques ?
Pour une forme de représentation du réel largement partagée, étayée par le témoignage de personnalités faisant autorité qui en confirment la criticité. Cela a donné naissance à une vision de la réalité qui, à première vue, semblerait inadaptée au langage médical ; en effet, des expressions telles que « environ 2 » ou « modérément » peuvent susciter une légitime perplexité et apparaître comme un retour anachronique à des concepts pré-scientifiques. Au contraire, cependant, l'utilisation de nombres flous ou d'assertions permet de traiter des données scientifiques dans des contextes où l'on ne peut pas parler de « probabilité » mais seulement de « possibilité ».[8]
Vérité fuzzy
Dans la tentative ambitieuse de traduire mathématiquement la rationalité humaine, on a pensé au milieu du XXe siècle d'élargir le concept de logique classique en formulant la logique floue. La logique floue concerne les propriétés que l'on pourrait appeler "gradualité", c'est-à-dire qui peuvent être attribuées à un objet avec des degrés différents. Des exemples sont les propriétés « être malade », « avoir des douleurs », « être grand », « être jeune », etc.
Mathématiquement, la logique floue permet d'attribuer à chaque proposition un degré de vérité compris entre et . L'exemple le plus classique pour expliquer cette notion est celui de l'âge : on peut dire qu'un nouveau-né a un « degré de jeunesse » égal à , dix-huit ans égal à , soixante ans égal à , etc.
Dans le contexte de la logique classique, par contre, les énoncés :
- un enfant de dix ans est jeune
- un trentenaire est jeune
sont tous les deux vrais. Or, dans le cas de la logique classique (qui n'admet que les deux données vraies ou fausses), cela signifierait que l'enfant et le trentenaire sont également jeunes. Ce qui est évidemment faux.
L'importance et le charme de la logique floue viennent du fait qu'elle est capable de traduire l'incertitude inhérente à certaines données du langage humain en formalisme mathématique, codant des concepts « élastiques » (tels que presque élevé, assez bon, etc.), en afin de les rendre compréhensibles et gérables par ordinateur.
Théorie des ensembles
Comme mentionné dans le chapitre précédent, le concept de base de la logique floue est celui de multivalence, c'est-à-dire, en termes de théorie des ensembles, de la possibilité qu'un objet puisse appartenir à un ensemble même partiellement et, donc, également à plusieurs ensembles avec des degrés différents . Rappelons d'emblée les éléments de base de la théorie des ensembles ordinaires. Comme on le verra, y figurent les expressions formelles des principes de la logique aristotélicienne, rappelés au chapitre précédent.
Quantificateurs
- Adhésion : représentée par le symbole 0 (appartient), - par exemple le nombre 13 appartient à l'ensemble des nombres impair
- Non-appartenance : représenté par le symbole (Il n'appartient pas)
- Inclusion : Représenté par le symbole (est contenu), - par exemple l'ensemble il est contenu dans l'ensemble plus large , (dans ce cas on dit que est un sous-ensemble de )
- Quantificateur universel, qui est indiqué par le symbole (pour chaque)
- Démonstration, qui est indiquée par le symbole (tel que)
Opérateurs d'ensemble
Etant donné tout l'univers nous indiquons par son élément générique de sorte que ; on considère alors deux sous-ensembles et internes à tels que et .
La théorie de la logique du langage flou est une extension de la théorie classique des ensembles dans laquelle, cependant, les principes de non-contradiction et du tiers exclu ne sont pas valables. Rappelons qu'en logique classique, étant donné l'ensemble et son complémentaire , le principe de non-contradiction énonce que si un élément appartient au tout il ne peut en même temps appartenir aussi à son complémentaire ; selon le principe du tiers exclu, cependant, l'union d'un entier et de son complémentaire constitue l'univers complet .
En d'autres termes, si un élément n'appartient pas au tout, il doit nécessairement appartenir à son complémentaire.
Ensemble fuzzy et membership function
Nous choisissons - comme formalisme - de représenter un ensemble flou avec le 'tilde':. Un ensemble flou est un ensemble où les éléments ont un « degré » d'appartenance (conformément à la logique floue) : certains peuvent être inclus dans l'ensemble à 100 %, d'autres dans des pourcentages inférieurs.
Pour représenter mathématiquement ce degré d'appartenance, on utilise la fonction appelée 'Membership Function'. La fonction est une fonction continue définie dans l'intervalle où elle vaut :
- si est totalement contenu dans (ces points sont appelés 'noyau', ils indiquent des valeurs de prédicat plausibles).
- si n'est pas contenu dans
- si est partiellement contenu dans (ces points sont appelés 'support', ils indiquent les valeurs possibles des prédicats).
La représentation graphique de la fonction peut être varié; de ceux avec des lignes linéaires (triangulaires, trapézoïdales) à ceux en forme de cloches ou de "S" (sigmoïdal) comme représenté sur la figure 1, qui contient tout le concept graphique de la fonction d'appartenance.[9][10]
L'ensemble support d'un ensemble flou est défini comme la zone dans laquelle résulte le degré d'appartenance; d'autre part, le noyau est défini comme la zone dans laquelle le degré d'appartenance prend la valeur .
Le 'Support set' représente les valeurs du prédicat jugées possibles, tandis que le 'core' représente celles jugées les plus plausibles.
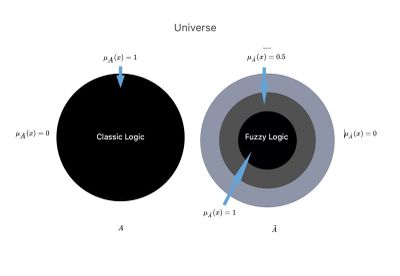
Si représentait un ensemble au sens ordinaire du terme ou de la logique du langage classique décrit précédemment, sa fonction d'appartenance ne pourrait prendre que les valeurs ou , selon que l'élément appartient ou non au tout considéré. La figure 2 montre une représentation graphique du concept net (rigidement défini) ou flou d'appartenance, qui rappelle clairement les considérations de Smuts.[11]
Revenons au cas particulier de notre Mary Poppins, dans laquelle nous voyons un décalage entre les affirmations du dentiste et du neurologue et nous cherchons une comparaison entre la logique classique et la logique floue :
Figure 2 : Imaginons l'univers scientifique dans lequel il y a deux mondes ou contextes parallèles, et .
Dans le contexte scientifique, le soi-disant « croustillant », et nous l'avons converti dans la logique du langage classique, dans lequel le médecin dispose d'une information de base scientifique absolue avec une ligne de démarcation claire que nous avons nommée .
Dans un autre contexte scientifique appelé « logique floue », et dans lequel il existe une union entre le sous-ensemble en que l'on peut aller jusqu'à dire : union entre .
On remarquera remarquablement les déductions suivantes :
- Logique classique dans le contexte dentaire dans laquelle seul un processus logique donnant comme résultat sera possible, ou étant la plage de données réduite aux connaissances de base dans l'ensemble . Cela signifie qu'en dehors du monde dentaire, il existe un vide et que le terme de la théorie des ensembles s'écrit précisément et qui est synonyme d'une gamme élevée de :
- Logique floue dans un contexte dentaire dans lequel ils sont représentés au-delà des connaissances de base du contexte dentaire également celles partiellement acquises du monde neurophysiologique auront la prérogative de rendre un résultat et un résultat à cause des connaissances de base qui à ce point est représenté par l'union de contextes dentaire et neurologique. Le résultat de cette mise en œuvre scientifique et clinique de la dentisterie permettrait une. «Réduction de l'erreur de diagnostic différentiel»
Considérations finales
Les sujets susceptibles de détourner l'attention du lecteur étaient, en fait, essentiels pour démontrer le message. Normalement, en effet, lorsqu'un esprit plus ou moins brillant se permet de jeter une pierre dans la mare de la Science, une onde de choc se produit, typique de la période de la science extraordinaire de Kuhn, contre laquelle rament la plupart des membres de la communauté scientifique internationale. En toute bonne foi, nous pouvons dire que ce phénomène — en ce qui concerne les sujets que nous abordons ici — est bien représenté dans la prémisse du début du chapitre.
Dans ces chapitres, en fait, un sujet fondamental pour la science a été abordé : la réévaluation, le poids spécifique qui a toujours été donné à , la prise de conscience des contextes scientifiques/cliniques , avoir entrepris un chemin plus élastique de Logique Floue que le Classique, réalisant l'extrême importance du et finalement l'union des contextes pour augmenter sa capacité diagnostique.[12][13]
Dans le prochain chapitre nous serons prêts à entreprendre un chemin tout aussi passionnant : il nous conduira dans le cadre d'une logique de Langage Système, et nous permettra d'approfondir nos connaissances, non plus seulement en sémiotique clinique, mais dans la compréhension du langage systémique. fonctions (récemment, il est en cours d'évaluation dans les disciplines neuromotrices pour la maladie de Parkinson).[14]
Dans Masticationpedia, bien sûr, nous rapporterons le sujet 'System Inference' dans le domaine du système masticatoire comme nous avons pu le lire dans le prochain chapitre intitulé 'System logical'.
- ↑ Takeuchi S, Okuda S, «Knowledge base toward understanding actionable alterations and realizing precision oncology», in Int J Clin Oncol, 2019».
PMID:30542800 - PMCID:PMC6373253
DOI:10.1007/s10147-018-1378-0
This is an Open Access resource! - ↑ Fuzzy logic on Pubmed
- ↑ All statistics collected following visits to the Pubmed site (https://pubmed.ncbi.nlm.nih.gov/). Last checked: December 2020.
- ↑ Temporomandibular Disorders in Pubmed
- ↑ Orofacial Pain in Pubmed
- ↑ Temporomandibular disorders AND Orofacial Pain in Pubmed
- ↑ "Temporomandibular disorders AND Orofacial Pain AND Fuzzy logic" in Pubmed
- ↑ Dubois D, Prade H, «Fundamentals of Fuzzy Sets», Kluwer Academic Publishers, 2000, Boston».
- ↑ Zhang W, Yang J, Fang Y, Chen H, Mao Y, Kumar M, «Analytical fuzzy approach to biological data analysis», in Saudi J Biol Sci, 2017».
PMID:28386181 - PMCID:PMC5372457
DOI:10.1016/j.sjbs.2017.01.027 - ↑ Lazar P, Jayapathy R, Torrents-Barrena J, Mol B, Mohanalin, Puig D, «Fuzzy-entropy threshold based on a complex wavelet denoising technique to diagnose Alzheimer disease», in Healthc Technol Lett, The Institution of Engineering and Technology, 2016».
PMID:30800318 - PMCID:PMC6371778
DOI:10.1049/htl.2016.0022 - ↑ •SMUTS J.C. 1926, Holism and Evolution, London: Macmillan.
- ↑ Mehrdad Farzandipour, Ehsan Nabovati, Soheila Saeedi, Esmaeil Fakharian. Fuzzy decision support systems to diagnose musculoskeletal disorders: A systematic literature review . Comput Methods Programs Biomed. 2018 Sep;163:101-109. doi: 10.1016/j.cmpb.2018.06.002. Epub 2018 Jun 6.
- ↑ Long Huang, Shaohua Xu, Kun Liu, Ruiping Yang, Lu Wu. A Fuzzy Radial Basis Adaptive Inference Network and Its Application to Time-Varying Signal Classification . Comput Intell Neurosci, 2021 Jun 23;2021:5528291.
doi: 10.1155/2021/5528291.eCollection 2021. - ↑ Mehrbakhsh Nilashi, Othman Ibrahim, Ali Ahani. Accuracy Improvement for Predicting Parkinson's Disease Progression. Sci Rep. 2016 Sep 30;6:34181. doi: 10.1038/srep34181.
particularly focusing on the field of the neurophysiology of the masticatory system













































![{\displaystyle [0;1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc3bf59a5da5d8181083b228c8933efbda133483)